
La valeur absolue en calcul est très utile pour résoudre divers problèmes mathématiques, à la fois dans les équations et les inégalités. Ce qui suit est une explication complète des valeurs absolues et des exemples de questions.
Définition de la valeur absolue
Tous les nombres ont leurs valeurs absolues respectives. Tous les nombres absolus sont positifs, donc les valeurs de nombre absolu des nombres avec le même nombre mais la différence entre les notations positive (+) et négative (-) auront le même résultat de nombre absolu.
Si x est membre d'un nombre réel, la valeur absolue s'écrit | x | et est défini comme suit:

"La valeur absolue est un nombre avec la même valeur de longueur ou de distance de l'origine ou du point zéro dans les coordonnées."
On peut interpréter que la valeur absolue de 5 est la longueur ou la distance du point 0 au point 5 ou (-5).
Les valeurs absolues de (-9) et 9 sont 9. La valeur absolue de 0 est 0, et ainsi de suite. Nilaa
Je vais absolument le comprendre en regardant l'image suivante:

Dans l'image ci-dessus, on peut comprendre que la valeur de | 5 | est la distance entre le point 5 et le nombre 0, soit 5, et | -5 | la distance entre le point (-5) et le numéro 0 est 5.
Si | x | représente la distance du point x à 0, alors | xa | est la distance entre le point x et le point a. Par exemple, lors de l'expression de la distance entre le point 5 et le point 2, il peut s'écrire | 5-2 | = 3

En général, on peut dire que la distance x à a peut être écrite avec la notation | xa | ou | hache |
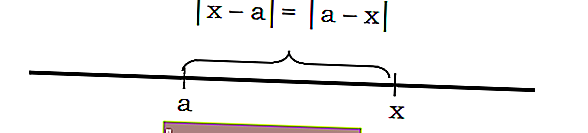
Par exemple, la distance d'un nombre au point 3 vaut 7 comme suit:
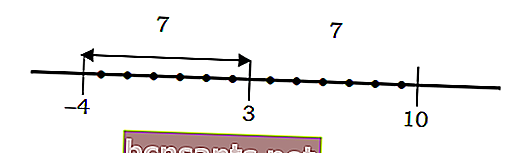
S'il est décrit dans l'équation algébrique | x-3 | = 7, il peut être résolu comme suit:
Lisez aussi: Mesurer les tremblements de terre avec des logarithmes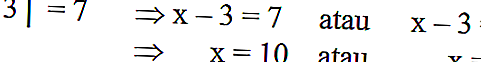
N'oubliez pas que | x-3 | est la distance du nombre x au point 3, où | x-3 | = 7 est la distance du nombre x au point 3 pour 7 unités.
Propriétés de la valeur absolue
Dans les opérations d'équation de nombres absolus, il existe des propriétés de nombres absolus qui peuvent aider à résoudre des équations de nombres absolus.
Voici les propriétés des nombres absolus en général dans les équations de valeur absolue:

Les propriétés de la valeur absolue de l'inégalité:
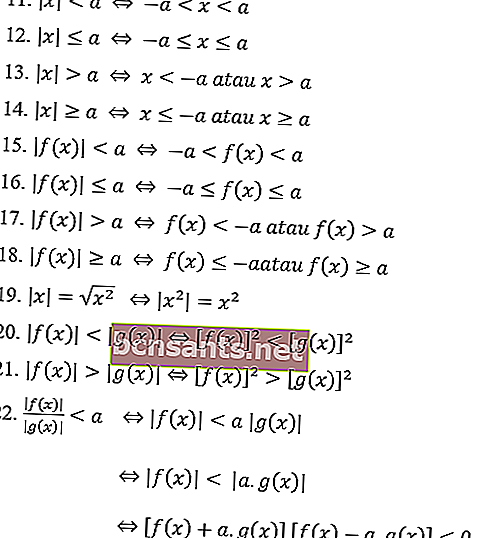
Exemples de problèmes d'équation de valeur absolue
Exemple de problème 1
Quelle est la valeur absolue de l'équation | 10-3 |?
Répondre:
| 10-3 | = | 7 | = 7
Exemple de problème 2
Quel est le résultat de x pour l'équation de la valeur absolue | x-6 | = 10?
Répondre:
Pour résoudre cette équation, il y a deux résultats possibles pour les nombres absolus
| x-6 | = 10
Première solution:
x-6 = 10
x = 16
deuxième solution:
x - 6 = -10
x = -4
Donc, la réponse à cette équation est 16 ou (-4)
Exemple de problème 3
Résolvez et calculez la valeur x dans l'équation suivante
–3 | x - 7 | + 2 = –13
Répondre:
–3 | x - 7 | + 2 = –13
–3 | x - 7 | = –13 - 2
–3 | x - 7 | = –15
| x - 7 | = –15 / –3
| x - 7 | = 5
Terminé jusqu'à la solution ci-dessus, alors la valeur x a deux valeurs
x - 7 = 5
x = 12
ou
x - 7 = - 5
x = 2
donc la valeur x finale est 12 ou 2
Exemple de problème 4
Résolvez l'équation suivante et quelle est la valeur x
| 7 - 2x | - 11 = 14
Répondre:
| 7 - 2x | - 11 = 14
| 7 - 2x | = 14 + 11
| 7 - 2x | = 25
Après avoir terminé l'équation ci-dessus, les nombres pour la valeur absolue de x sont les suivants
7 - 2x = 25
2x = - 18
x = - 9
ou
7 - 2x = - 25
2x = 32
x = 16
La valeur x finale est donc (- 9) ou 16
Exemple de problème 5
Trouvez la solution à l'équation de valeur absolue suivante:
| 4x - 2 | = | x + 7 |
Répondre:
Pour résoudre l'équation ci-dessus, utilisez deux solutions possibles, à savoir:
Lire aussi: Erreurs dans la lecture des résultats statistiques de l'enquête sur l'éligibilité des candidats à la présidentielle4x - 2 = x + 7
x = 3
ou
4x - 2 = - (x + 7)
x = - 1
Donc, la solution de l'équation | 4x - 2 | = | x + 7 | est x = 3 ou x = - 1
Exemple de problème 6
Déterminez la solution de l'équation de valeur absolue suivante:
| 3x + 2 | ² + | 3x + 2 | - 2 = 0
Quelle est la valeur de x?
Répondre:
Simplification: | 3x + 2 | = p
puis
| 3x + 2 | ² + | 3x + 2 | -2 = 0
p² + p - 2 = 0
(p + 2) (p - 1) = 0
p + 2 = 0
p = - 2 (la valeur absolue n'est pas négative)
ou
p - 1 = 0
p = 1
| 3x + 2 | = 1
Jusqu'à la solution ci-dessus, il y a 2 réponses possibles pour x, à savoir:
3x + 2 = 1
3x = 1 - 2
3x = - 1
x = - 1/3
ou
- (3x + 2) = 1
3x + 2 = - 1
3x = - 1 - 2
3x = - 3
x = - 1
La solution de l'équation est donc x = - 1/3 ou x = - 1
Référence: Valeur absolue - Les mathématiques sont amusantes
