
La fréquence attendue estle nombre d'apparitions attendues à un événement en menant à plusieurs reprises des expériences qui sont également appelées tests expérimentaux.
Ou le produit du hasard de l'événement, par exemple, l'événement A avec le nombre d'expériences effectuées.
En termes simples, avez-vous déjà joué à Ludo? Lancez deux dés en même temps et attendez-vous à ce qu'un six apparaisse sur les deux dés? Si c'est le cas, cela signifie que vous avez appliqué la théorie de la fréquence attendue .
Formules de fréquences attendues
En général, la formule de la fréquence attendue est la suivante:
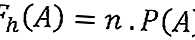
Information:
F h (A) = la fréquence attendue d'un événement A
n = nombre d'occurrences A
P (A) = probabilité d'un événement A.
Exemples de questions de fréquence attendues
Exemple de problème 1
- Les deux dés sont lancés ensemble 144 fois. Déterminez la chance que l'espoir naisse
- Les six sur les deux meurent.
- Le nombre totalise six sur les deux dés.
Solution:
Pour résoudre un problème comme celui-ci, calculez d'abord le nombre total d'occurrences. Tous les événements sont notés S, alors:
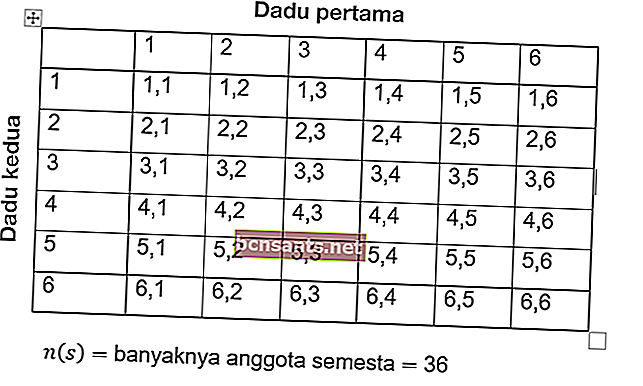
De sorte que le nombre de membres de l'univers des nombres est n (s) = 36.
1. L'apparition du chiffre six sur les deux dés.
Pour les deux nombres qui n'apparaissent qu'un seul, à savoir (6,6), alors:
n (1) = 1
Le nombre d'expériences était de 144 fois, alors
n = 144
Donc,
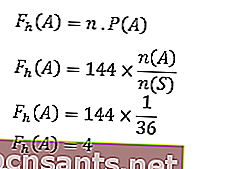
Ainsi, la fréquence attendue d'apparition du nombre six sur les deux dés est de 4 fois.
2. L'apparition du nombre de dés totalisant six
Pour le nombre de dés totalisant six, à savoir

Le nombre d'expériences était de 144 fois, alors

Donc,

Ainsi, la fréquence attendue d'apparition d'un six dés est de 20 fois.
Exemple de problème 2
Une pièce qui a été jetée en l'air 30 fois. Déterminez la fréquence d'apparition attendue du côté numérique.
Lisez également: Formules d'accélération + exemples de problèmes et de solutionsSolution:
L'univers de cet incident n'est que de deux, à savoir le côté numérique et le côté image, ou écrit

alors, n (S) = 2
Le nombre de pièces lancées est de 30 fois, alors n = 30
Il n'y a qu'un seul côté d'un nombre, donc n (A) = 1
La fréquence prévue des événements est,
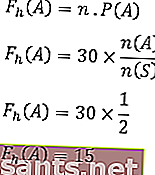
Ainsi, la fréquence d'apparition attendue du côté numérique est de 20 fois.
Conclusion
La fréquence attendue est donc une fréquence ou le nombre d'essais multiplié par la probabilité d'un événement afin que le nombre d'attentes apparaisse sur un événement particulier.
Alors, après l'explication ci-dessus, pouvez-vous calculer vos espoirs de gagner à la loterie? Quelles astuces devez-vous faire pour que vos espoirs de gagner soient élevés?
Écrivez votre astuce infaillible dans les commentaires et faites-leur savoir.
Ainsi, une explication de la formule et de la compréhension ainsi que des exemples de la fréquence des attentes, j'espère que cela sera utile et à vous voir dans le prochain matériel
