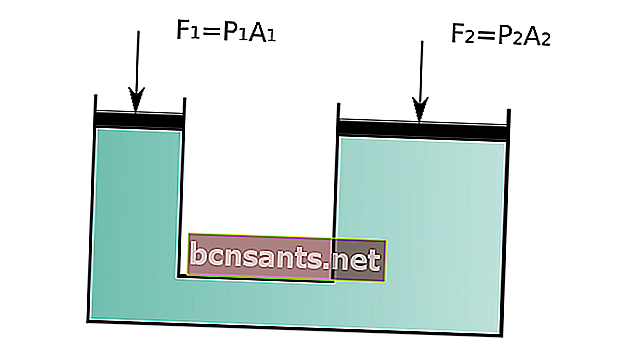
La loi de Pascal se lit comme suit: "Si une pression externe est appliquée à un système fermé, la pression en tout point du fluide augmentera proportionnellement à la pression externe appliquée."
Avez-vous déjà vu un atelier de réparation changer de pneus? Si c'est le cas, vous verrez sûrement que la voiture ou même le camion est d'abord soulevée à l'aide d'un petit outil appelé cric.
Bien sûr, la question se pose de savoir comment un cric peut soulever une voiture qui pèse même des milliers de fois du cric.

La réponse à cette question est expliquée par une loi appelée loi de Pascal. Pour plus de détails, regardons plus en détail la loi de Pascal avec un exemple du problème.
Comprendre la loi de Pascal
Au 16ème siècle, un philosophe et scientifique du nom de Blaise Pascal a inventé une loi appelée loi de Pascal. Cette loi se lit comme suit:
"Si une pression externe est appliquée à un système fermé, la pression en tout point du fluide augmentera proportionnellement à la pression appliquée de l'extérieur."
La science fondamentale de cette loi est la pression, où la pression appliquée au fluide avec un système fermé sera égale à la pression sortant du système.
Grâce à lui, des innovations ont alors commencé à apparaître notamment pour résoudre le problème du levage d'une charge lourde. Des exemples sont des vérins, des pompes et des systèmes hydrauliques de freinage.
Formule
Avant de passer aux équations ou formules de la loi de Pascal, nous devons apprendre la science fondamentale, à savoir la pression. La définition générale de la pression est l'effet ou d'une force agissant sur une surface. La formule générale de l'équation est:
P = F / A
Où :
P est la pression (Pa)
F est la force (N)
A est la surface effective (m2)
L'équation mathématique de la loi de Pascal est très simple où:
Lire aussi: Structure bactérienne, fonction et images [COMPLET]Enter = Quitter
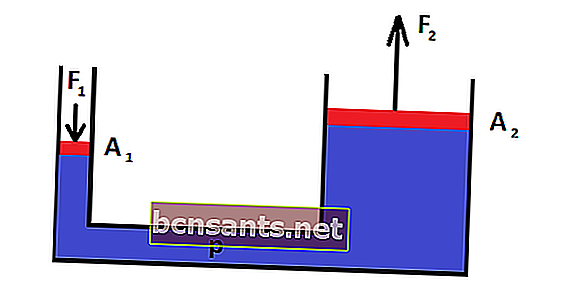
Avec l'image ci-dessus, l'équation de la loi de Pascal peut s'écrire:
P1 = P2
F1 / A1 = F2 / A2
Avec:
P1: pression d'entrée (Pa)
P2: pression de sortie (Pa)
F1: force appliquée (N)
F2: force produite (N)
A1: aire de force appliquée (m2)
A2: surface résultante (m2)
En outre, il existe un autre terme utilisé dans l'application de la loi de Pascal qui est appelé avantage mécanique. En général, l'avantage mécanique est le rapport entre la force qu'un système peut produire et la force qui doit être appliquée. Mathématiquement, l'avantage mécanique peut s'écrire:
avantage mécanique = F2 / F1
Comme dans l'exemple d'un monte-voiture hydraulique, le fluide dans le système aura toujours le même volume.

Par conséquent, l'équation de la loi de Pascal peut également être écrite comme un rapport de volume entrant et sortant qui:
V1 = V2
ou peut être écrit comme
A1.h1 = A2.h2
Où :
V1 = volume enfoncé
V2 = volume qui sort
A1 = zone de la section d'entrée
A2 = zone de section de sortie
h1 = profondeur de la section entrante
h2 = hauteur de la section de sortie
Exemple de problèmes
Voici quelques exemples et discussions de problèmes liés à l'application de la loi de Pascal afin que vous puissiez comprendre plus facilement.
Exemple 1
Un levier hydraulique permet de soulever une charge de 1 tonne. Si le rapport entre les sections transversales est de 1: 200, quelle est la force minimale à appliquer sur le levier hydraulique?
Répondre:
A1 / A2 = 1: 200
m = 1000 kg, alors W = m. g = 1000. 10 = 10 000 N
F1 / A1 = F2 / A2
F1 / F2 = A1 / A2
F1 / 10000 = 1/200
F1 = 50N
Donc, la force que le système doit faire est de 50N
Exemple 2
L'avantage mécanique d'un levier hydraulique a une valeur de 20. Si une personne veut soulever une voiture pesant 879 kg, quelle force le système doit-il faire?
Répondre:
m = 879 kg, alors W = mg = 879. 10 = 8790 N
gain mécanique = 20
F2 / F1 = 20
8790 / F1 = 20
F1 = 439,5 N
donc la force exercée sur le levier est de 439,5 N
Lisez aussi: 1 an combien de semaines? (Années en semaines) Voici la réponseExemple 3
Un levier hydraulique a un diamètre de piston d'entrée de 14 cm et un diamètre de sortie de 42 cm. Si le piston descend à une profondeur de 10 cm, quelle est la hauteur du piston qui est soulevé?
Répondre:
Le piston a une surface circulaire de sorte que sa surface est
A1 = π. r12 = 22/7. (14/2) 2 = 154 cm2
A2 = π. r22 = 22/7. (42/2) 2 = 1386 cm2
h1 = 10 cm
puis
A1. h1 = A2. h2
154. 10 = 1386. h2
h2 = 1540/1386
h2 = 1,11 cm
Ainsi, le piston qui est soulevé mesure 1,11 cm de haut
Exemple 4
Un compresseur avec un tuyau fixé à un robinet a un diamètre de 14 mm. Si un pulvérisateur avec une buse de 0,42 mm est installé à l'extrémité du tuyau et lorsque le compresseur est mis en marche, la pression est mesurée à 10 bars. Déterminez la quantité de force d'échappement d'air qui sort de la buse si la pression du compresseur ne diminue pas.
Réponse :
Les tuyaux et les trous ont une section transversale circulaire
Ensuite, la zone de la surface du trou est
A2 = π. r22 = 22/7. (1,4 / 2) 2 = 1,54 mm2
"N'oubliez pas que la loi de Pascal explique que la pression à l'intérieur est égale à la pression à la sortie."
Pour que l'armée de l'air sortante soit:
P = F / A
F = P. UNE
F = 10 bar. 1,54 mm2
changer la barre d'unité en pascal et mm2 en m2
puis
F = 106 Pa. 1,54 x 10 à 6 m2
F = 1,54 N
Donc la force du vent qui sort est de 1,54 N
Ainsi la discussion sur la loi de Pascal, j'espère qu'elle pourra vous être utile.
