
Le périmètre du triangle est la longueur totale du côté du triangle. Par conséquent, la formule pour le périmètre du triangle est K = a + b + c ou la somme de tous les côtés du triangle.
Lorsque vous faites le tour du jardin triangulaire, qu'est-ce que cela signifie? Oui! Vous encerclez une forme de triangle. Qu'est-ce qu'une forme de triangle plat? Ce qui suit est une explication du triangle, le type de triangle et comment déterminer ou la formule pour le périmètre du triangle.
Explication du triangle
Un triangle est une forme formée de trois lignes qui se croisent formant un angle. Le nombre d'angles dans un triangle est de 180 degrés.
Les triangles sont les formes plates les plus simples car ce sont les éléments qui forment d'autres formes plates telles que des carrés, des rectangles, des cercles et des éléments de formes plates qui forment des formes telles que des prismes et des pyramides.
Caractéristiques d'un triangle
Pour expliquer plus en détail la signification d'un triangle, je vais dessiner une forme de triangle arbitraire ABC ci-dessous:
Les éléments du triangle ABC comprennent:
- Les points A, B et C sont appelés sommets.
- Les lignes AB, BC et CA sont appelées les côtés du triangle.
- Les différents triangles peuvent être vus à partir des longueurs latérales et des angles formés par le triangle.
Types de triangles
Les types de triangles varient considérablement en fonction de la longueur des côtés et des angles qui forment le triangle. Ce qui suit est la division des types de triangles
Types de triangles basés sur la longueur des côtés
- Triangle équilatéral
À savoir un triangle avec les trois côtés de la même longueur. De plus, les trois angles formés par le triangle latéral ont la même taille, qui est de 60 degrés, car le nombre d'angles du triangle est de 180 degrés.
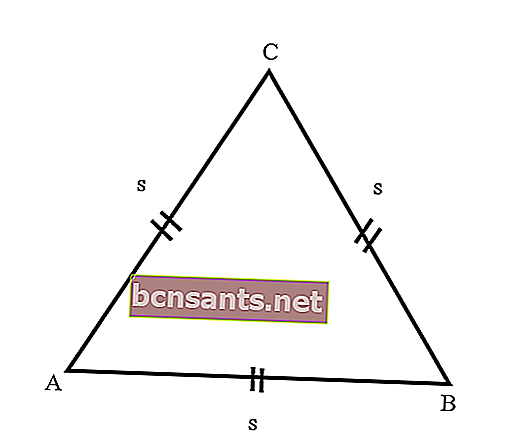
Pour en savoir plus sur les triangles équilatéraux, considérons l'explication suivante des propriétés des triangles équilatéraux:

Dans la figure (b) - (d), il apparaît que la forme du triangle ABC peut occuper son cadre exactement en utilisant 3 façons, à savoir, tourné jusqu'à 120 degrés centré sur le point O (regardez le sens de rotation) sur (figure b) tourné jusqu'à 240 degrés au centre de rotation en O (sur la figure c) qui est tourné de 360 degrés (un tour complet) au point central en O (sur la figure d).
Lisez aussi: Formules d'opportunités et exemples de problèmesConformément à l'explication des figures a à f, le triangle équilatéral ABC a une symétrie de rotation jusqu'au niveau 3. Pendant ce temps, les figures e, f et g inversées peuvent occuper correctement le cadre. Pour cela, la forme du triangle ABC possède 3 axes de symétrie. Alors que dans l'image ci-dessus, les axes de symétrie sont CD, BF et AE. Pour que le triangle équilatéral puisse occuper le cadre exactement de 6 façons.
Sur la base de certaines des descriptions ci-dessus, certaines des propriétés qui existent dans un triangle équilatéral comprennent: il a 3 niveaux de symétrie de rotation, 3 axes de symétrie, 3 côtés équilatéraux, 3 angles égaux de 60 degrés et peut occuper le cadre de 6 façons maximum.
- Triangle isocèle
À savoir un triangle avec un côté de la même longueur. Un triangle isocèle a deux angles égaux, c'est-à-dire des angles se faisant face.
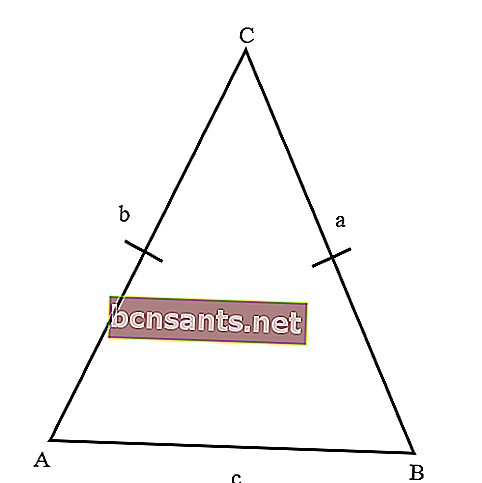
Voici les propriétés du triangle isocèle;
- La construction d'un triangle isocèle, tourné pendant un tour complet, occupe le cadre exactement dans un sens. Pour que le triangle de samakaki ait une symétrie de rotation de un.
- Pendant ce temps, un triangle isocèle n'a qu'un seul axe de symétrie.
- Tout triangle
À savoir un triangle dont les trois côtés n'ont pas la même longueur et les trois angles ne sont pas égaux.

Voici les propriétés de n'importe quel triangle:
- A trois côtés qui ne sont pas de la même longueur. (Dans l'image ci-dessus, les trois côtés sont censés être de longueur BA ≠ CB ≠ AC).
- N'a pas de symétrie de pli.
- A une seule symétrie tournante.
- Les trois coins ont des tailles différentes.
Types de triangles basés sur l'angle
- Triangle aigu
À savoir un triangle avec les trois angles formant un angle aigu. Un angle aigu est un angle compris entre 0 et 90 degrés.
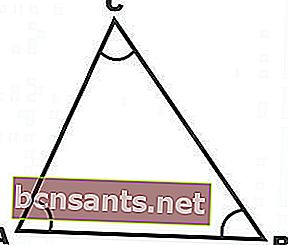
- Triangle émoussé
A savoir un triangle avec un coin formant un angle obtus. Un angle obtus est un angle dont la magnitude est comprise entre 90 et 180 degrés.
Lisez aussi: Solutions pour les formules souvent oubliées!
- Triangle rectangle
À savoir un triangle dont l'un des coins forme un angle de 90 degrés.
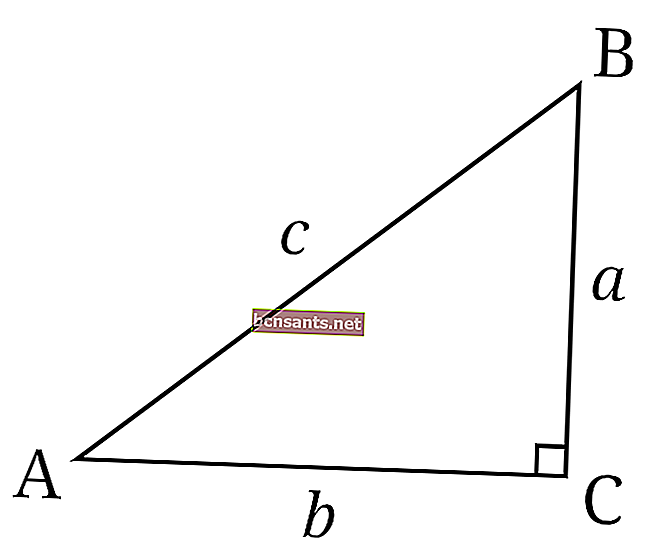
La formule pour le périmètre d'un triangle
Le périmètre de la forme est obtenu à partir du nombre de longueurs des arêtes (sisis) qui forment la forme.
Ainsi, la formule pour le périmètre d'un triangle peut être obtenue en additionnant chaque côté du triangle.
Périmètre du triangle = longueur du 1er côté + longueur du 2ème côté + longueur du 3ème côté
K = a + b + c
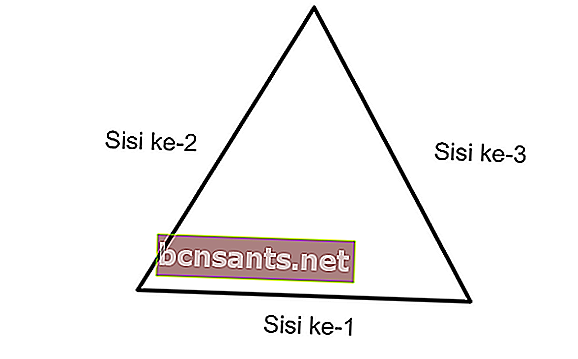
Exemple de problème pour trouver le périmètre d'un triangle
Exemple de problème 1.
Un triangle équilatéral a une longueur de côté de 3 cm, quelle est la circonférence!
Solution:
Vous savez: s = 3 cm
Recherché: périmètre du triangle?
Répondre:
Les triangles équilatéraux ont les mêmes côtés,
K = s + s + s
K = 3 + 3 + 3
K = 9 cm
Ainsi, le périmètre du triangle équilatéral est de 9 cm.
Exemple de problème 2.
Un triangle isocèle a une longueur totale de côté de 36 cm. Le côté le plus long mesure 13 cm. Quelle est la longueur du côté le plus court?
Solution:
Vous savez que = K = 36 cm; b = a = 13 cm
Recherché : La longueur du côté le plus court?
Réponse :
Périmètre du triangle = a + b + c
36 = 13 + 13 + c
c = 10 cm
Ainsi, la longueur du côté le plus court du triangle est de 10 cm
Exemple de problème 3.
On vous donne n'importe quel triangle avec des côtés de 9, 11, 13 cm chacun. Calculez le périmètre du triangle!
Solution:
On sait que : a = 13 cm; b = 9 cm; c = 11 cm
Recherché : périmètre du triangle?
Répondre:
K = a + b + c
K = 13 +9 +11
K = 33 cm
Ainsi, le périmètre du triangle est de 33 cm
Exemple de problème 4.
Calculez le périmètre du triangle isocèle avec une aire de 12 cm2 et la longueur des côtés de 6 cm!
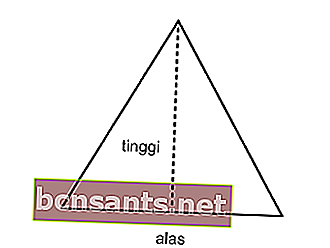
Solution:
Vous savez: L = 12 cm2; a = 6 cm
Recherché: périmètre du triangle?
Répondre:
Pour trouver le périmètre du triangle, vous devez connaître la longueur des côtés du triangle.
Utilisez la zone pour trouver la hauteur du triangle
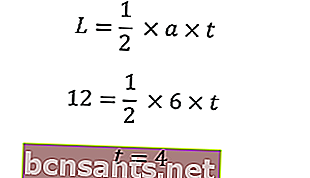
En utilisant le système de Pythagore, on connaît l'hypoténuse d'un triangle isocèle en entrant la longueur de la base (a) et la hauteur du triangle (t)

En utilisant l'équation ci-dessus, nous obtenons l'hypoténuse du triangle
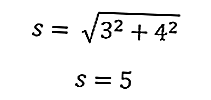
Cela vous permettra de calculer le périmètre du triangle immédiatement
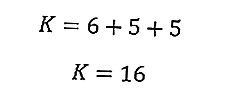
Ainsi, le périmètre du triangle est de 16 cm
Référence : Triangle - Math is Fun
