
L'équation quadratique est l'une des équations mathématiques de la variable qui a la plus grande puissance de deux.
La forme générale d'une équation quadratique ou PK est la suivante:
hache 2 + bx + c = 0
où x est la variable, a , b est le coefficient et c est la constante. La valeur de a n'est pas égale à zéro.
Formes graphiques
Si une équation quadratique est décrite en termes de coordonnées cartésiennes (x, y), elle formera un graphe parabolique. Par conséquent, les équations quadratiques sont aussi souvent appelées équations paraboliques .
Voici un exemple de la forme de cette équation sous la forme d'un graphe parabolique.
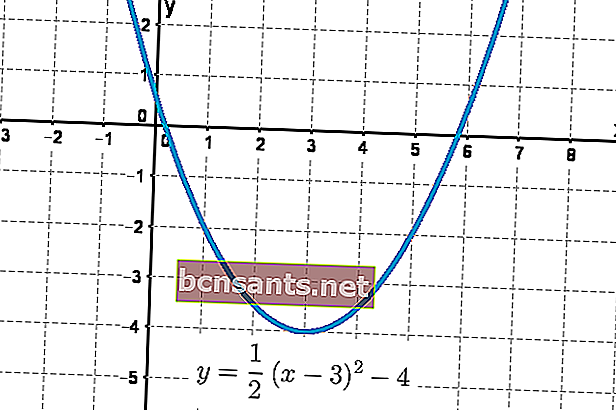
Dans l'équation générale, les valeurs de a , b et c affectent grandement le modèle parabolique résultant.
La valeur de a détermine la courbe concave ou convexe de la parabole. Si la valeur de a> 0, alors la parabole s'ouvrira (concave) . Inversement, si a <0 , alors la parabole s'ouvrira vers le bas (convexe) .

La valeur de b dans l'équation détermine le sommet de la parabole . En d'autres termes, déterminez la valeur de l'axe de la symétrie de la courbe qui est égale à x = - b / 2a .

La valeur constante c sur le graphique de l'équation détermine le point d'intersection de la fonction parabole sur l'axe y . Ce qui suit est un graphique parabolique avec les changements de la valeur constante c .

Racines de l'équation quadratique (PK)
La solution d'une équation quadratique est appelée un kar - la racine de l'équation quadratique .
Diverses racines PK
Les types de racines PK peuvent être trouvés facilement en utilisant la formule générale D = b2 - 4ac de l'équation générale pour l'axe quadratique ax2 + bx + c = 0.
Voici les types de racines d'équations quadratiques.
1. Racine réelle (D> 0)
Si la valeur de D> 0 à partir d'un PK, cela produira des racines d'équation réelles mais avec des racines différentes. En d'autres termes, x1 n'est pas la même chose que x2.
Exemple de l'équation racine réelle (D> 0)
Trouvez le type de racine de l'équation x2 + 4x + 2 = 0.
Solution:
a = 1; b = 4; et c = 2
D = b2 - 4ac
D = 42 - 4 (1) (2)
D = 16 - 8
D = 8
Donc, puisque la valeur de D> 0, alors la racine est de type racine réelle.
2. racine réelle égale x1 = x2 (D = 0)
Est un type de racine d'une équation quadratique qui produit des racines de même valeur (x1 = x2).
Exemple de racines réelles (D = 0)
Trouvez la valeur racine PK de 2x2 + 4x + 2 = 0.
Lisez aussi: Types de cycles d'eau (+ Image complète et explication)Solution:
a = 2; b = 4; c = 2
D = b2 - 4ac
D = 42 - 4 (2) (2)
D = 16 - 16
D = 0
Donc, parce que la valeur de D = 0, il est prouvé que les racines sont réelles et jumelées.
3. Racines imaginaires / non réelles (D <0)
Si la valeur de D <0, alors la racine de l'équation quadratique sera imaginaire / non réelle.
Exemple de racines imaginaires (D <0) /
Trouvez le type de racine de l'équation x2 + 2x + 4 = 0.
Solution:
a = 1; b = 2; c = 4
D = b2 - 4ac
D = 22 - 4 (1) (4)
D = 4 - 16
D = -12
Donc, puisque la valeur de D <0, la racine de l'équation est une racine irréelle ou imaginaire.
Trouvez les racines de l'équation quadratique
Il existe plusieurs méthodes qui peuvent être utilisées pour trouver les racines d'une équation quadratique. Parmi eux se trouvent la factorisation, les carrés parfaits et l'utilisation de la formule abc.
Ce qui suit décrit plusieurs méthodes de recherche des racines d'équation.
1. Factorisation
La factorisation / factorisation est une méthode pour trouver les racines en recherchant une valeur qui, si multipliée, produira une autre valeur.
Il existe trois formes d'équations quadratiques (PK) avec une factorisation de racine différente, à savoir:
| Non. | Forme d'équation | Factorisation racine-racine |
| 1 | x 2 + 2xy + y 2 = 0 | (x + y) 2 = 0 |
| 2 | x 2 - 2xy + y 2 = 0 | (x - y) 2 = 0 |
| 3 | x 2 - y 2 = 0 | (x + y) (x - y) = 0 |
Voici un exemple de problème d'utilisation de la méthode de factorisation dans les équations quadratiques.
Résolvez l'équation quadratique 5x 2 + 13x + 6 = 0 en utilisant la méthode de factorisation.
Solution:
5x2 + 13x = 6 = 0
5x2 + 10x + 3x + 6 = 0
5x (x + 2) + 3 (x + 2) = 0
(5x + 3) (x + 2) = 0
5x = -3 ou x = -2
Donc, la solution sera x = -3/5 ou x = -2
2. Carrés parfaits
La forme quadratique parfaite est une équation quadratique qui produit des nombres rationnels .
Les résultats d'une équation quadratique parfaite utilisent généralement la formule suivante:
(x + p) 2 = x2 + 2px + p2
La solution générale de l'équation quadratique parfaite est la suivante:
(x + p) 2 = x2 + 2px + p2
avec (x + p) 2 = q, alors:
(x + p) 2 = q
x + p = ± q
x = -p ± q
Voici un exemple de problème lié à l'utilisation de la méthode de l'équation parfaite.
Résolvez l'équation x2 + 6x + 5 = 0 en utilisant la méthode de l'équation quadratique parfaite!
Solution:
x2 + 6x +5 = 0
x2 + 6x = -5
L'étape suivante consiste à ajouter un nombre sur les côtés droit et gauche afin qu'il puisse se transformer en un carré parfait.
x2 + 6x + 9 = -5 + 9
x2 + 6x + 9 = 4
(x + 3) 2 = 4
(x + 3) = √4
x = 3 ± 2
Donc, le résultat final est x = -1 ou x = -5
Lisez aussi: Définition et différence des homonymes, homophones et homographes3. Formules quadratiques ABC
La formule abc est un choix alternatif lorsque l'équation quadratique ne peut pas être résolue par factorisation ou par des méthodes quadratiques parfaites.
Voici la formule abc de l'équation quadratique ax2 + bx + c = 0.
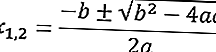
Voici un exemple de résolution d'un problème d'équation quadratique à l'aide de la formule abc .
Résolvez l'équation x2 + 4x - 12 = 0 en utilisant la méthode de formule abc!
Solution:
x2 + 4x - 12 = 0
où a = 1, b = 4, c = -12

Construire une nouvelle équation quadratique
Si nous avons déjà appris à trouver les racines de l'équation, nous allons maintenant apprendre à composer l'équation quadratique à partir des racines précédemment connues.
Voici quelques façons de créer un nouveau PK.
1. Construisez des équations lorsque les racines sont connues
Si une équation a des racines x1 et x2, alors l'équation de ces racines peut être exprimée en termes de
(x- x 1 ) (x- x 2 ) = 0
Exemple:
Trouvez une équation quadratique où les racines sont comprises entre -2 et 3.
Solution:
x 1 = -2 et x 2 = 3
(x - (- 2)) (x-3) = 0
(x + 2) (x + 3)
x2-3x + 2x-6 = 0
x2-x-6 = 0
Donc, le résultat de l'équation pour ces racines est x2-x-6 = 0
2. Construisez une équation quadratique si vous connaissez le nombre et le produit des racines
Si les racines de l'équation quadratique avec le nombre et les temps x1 et x2 sont connues, l'équation quadratique peut être convertie sous la forme suivante.
x2- (x 1+ x 2 ) x + (x 1. x 2 ) = 0
Exemple:
Trouvez une équation quadratique avec des racines 3 et 1/2.
Solution:
x 1 = 3 et x 2 = -1/2
x 1+ x 2 = 3 -1/2 = 6/2 - 1/2 = 5/2
x 1. x 2 = 3 (-1/2) = -3/2
Ainsi, l'équation quadratique est:
x2- (x 1+ x 2 ) x + (x 1. x 2 ) = 0
x2– 5/2 x - 3/2 = 0 (chaque côté multiplié par 2)
2x2-5x-3 = 0
Ainsi, l'équation quadratique pour les racines 3 et 1/2 est 2x2-5x-3 = 0.
