
La formule de Pythagore est une formule utilisée pour trouver l'une des longueurs d'un triangle.
La formule de Pythagore, également connue sous le nom de théorème de Pythagore, est l'une des premières matières enseignées en mathématiques.
Depuis l'école primaire, on nous enseigne cette formule de Pythagore.
Dans cet article, je revisiterai la proposition du théorème de Pythagore avec des exemples de problèmes et leurs solutions.
Histoire de Pythagore - Pythagore
En fait, Pythagore est le nom d'une personne de la Grèce antique de 570 à 495 av.
Pythagore était un brillant philosophe et mathématicien de son temps. Ceci est démontré par ses découvertes qui ont réussi à résoudre le problème de la longueur des côtés du triangle avec une formule très simple.
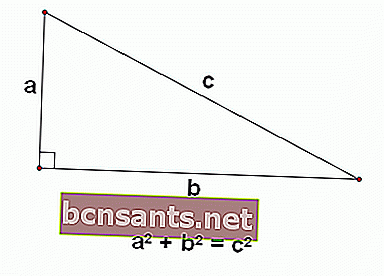
Théorème de Pythagore
Le théorème de Pythagore est une proposition mathématique sur les triangles rectangles, qui montre que la longueur de la base du carré plus la longueur de la hauteur du carré est égale à la longueur de l'hypoténuse du carré.
Supposer….
- La longueur de la base du triangle est un
- La longueur de la hauteur est b
- La longueur de l'hypoténuse est de c
Ainsi, en utilisant l'argument de Pytaghoras, la relation entre les trois peut être formulée pour être
a 2 + b 2 = c 2
Preuve du théorème de Pythagore
Si vous êtes observateur, vous pourrez imaginer qu'au fond la formule des pytaghoras montre que l'aire d'un carré de côté a plus l'aire d'un carré de côté b est égale à l'aire d'un carré de côté c.
Vous pouvez voir l'illustration dans l'image suivante:

Vous pouvez également le regarder dans une vidéo comme celle-ci
Comment utiliser la formule de Pythagore
La formule phytagorienne a 2 + b 2 = c 2 peut fondamentalement être exprimée sous plusieurs formes, à savoir:
a2 + b2 = c2
c2 = a 2 + b 2
a2 = c2 - b 2
b2 = c2 -a2
Pour résoudre chacune de ces formules, vous pouvez utiliser la valeur racine de la formule de Pythagore ci-dessus.
Lisez aussi: Microscope: explication, ses composants et sa fonction
Remarque importante: n'oubliez pas que les formules ci-dessus ne s'appliquent qu'aux triangles rectangles. Sinon, alors non valide.
Triple Pythagore (modèle numérique)
Le triple de Pythagore est le nom du modèle de nombre abc qui répond à la formule de Pythagore ci-dessus.
Il y a tellement de nombres qui remplissent ce triple pytaghoras, même jusqu'à de très grands nombres.
Quelques exemples incluent:
- 3 - 4 - 5
- 5 - 12 - 13
- 6 - 8 - 10
- 7 - 24 - 25
- 8 - 15 - 17
- 9 - 12 - 15
- 10 - 24 - 26
- 12 - 16 - 20
- 14 - 48 - 50
- 15 - 20 - 25
- 15 - 36 - 39
- 16 - 30 - 34
- 17 - 144 - 145
- 19 - 180 - 181
- 20 - 21 - 29
- 20 - 99 - 101
- 21 - 220 - 221
- 23 - 264 - 265
- 24 –143 - 145
- 25 - 312 - 313
- etc
La liste peut encore être prolongée jusqu'à un très grand nombre.
En substance, les nombres correspondront lorsque vous branchez les valeurs dans la formule a 2 + b 2 = c 2
Exemples de questions complètes et de discussion
Afin de mieux comprendre le sujet de cette formule de Pytaghoras, regardons l'exemple de la question complète et sa discussion ci-dessous.
Exemple de formule 1 de Pythagore
1. Un triangle a un côté BC de 6 cm de long et un côté AC de 8 cm , combien de cm fait l'hypoténuse du triangle (AB)?
Solution:
Connu :
- BC = 6 cm
- AC = 8 cm
Recherché: longueur AB?
Répondre:
AB2 = BC2 + AC2
= 62 + 82
= 36 + 64
= 100
AB = √100
= 10
Ainsi, la longueur du côté AB (oblique) est de 10 cm.
Exemple du théorème de Pythagore 2
2. On sait qu'un triangle a une hypoténuse de 25 cm de long et le côté vertical du triangle a une longueur de 20 cm . Quelle est la longueur du côté plat?
Solution:
C'est connu: nous faisons un exemple, pour le rendre plus facile
- c = hypoténuse, b = côté plat, a = côté vertical
- c = 25 cm, a = 20 cm
Recherché: La longueur du côté plat (b)?
Répondre:
b2 = c2 - a2
= 252 - 202
= 625 - 400
= 225
b = √225
= 15 cm
Pour que la longueur du côté plat du triangle soit de 15 cm .
Exemple de formule 3 de Pythagore
3. Quelle est la longueur du côté vertical d'un triangle si vous savez que l'hypoténuse du triangle mesure 20 cm et que le côté plat a une longueur de 16 cm .
Solution :
C'est connu: on fait d'abord l'exemple et la valeur
- c = hypoténuse, b = côté plat, a = côté vertical
- c = 20 cm , b = 16 cm
Recherché: La longueur de la verticale (a)?
Répondre:
a2 = c2 - b2
= 202 - 162
= 400 - 256
= 144
a = √144
= 12 cm
À partir de là, vous obtenez la longueur du côté du triangle qui est droit est de 12 cm .
Exemple de problème de triple Pythagore 4
Continuez la valeur du triple de Pythagore suivant….
3, 4,….
6, 8,….
5, 12,….
Solution:
Tout comme les solutions des problèmes précédents, cette triple relation de Pythagore peut être résolue en utilisant la formule c2 = a 2 + b 2.
Veuillez essayer de le calculer vous-même….
La réponse (à faire correspondre) est:
- 5
- dix
- 13
Exemple de formule de Pythagore Problème 5
Étant donné que trois villes (A, B, C) forment un triangle, avec des coudes dans la ville B.
Distance de la ville AB = 6 km, distance de la ville BC = 8 km, à quelle distance se trouve la ville AC?
Solution:
Vous pouvez utiliser la formule du théorème de Pythagore et obtenir le résultat du calcul de la distance de la ville AC = 10 km.
Ainsi la discussion de la formule de Pythagore - les arguments du théorème de Pythaghoras qui est présenté simplement. J'espère que vous pourrez bien le comprendre, de sorte que plus tard, vous puissiez comprendre d'autres sujets mathématiques, tels que la trigonométrie, les logarithmes, etc.
Si vous avez encore des questions, vous pouvez les soumettre directement dans la colonne des commentaires.
Référence
- Quelle est la proposition de Pythagore? - Fils demandé
- Théorème de Pythagore - Les mathématiques sont amusantes
