
L'équation du cercle a la forme générale x ^ 2 + y ^ 2 + Ax + By + C = 0, qui peut être utilisée pour déterminer le rayon et le centre d'un cercle.
L'équation du cercle que vous apprendrez ci-dessous a plusieurs formes. Dans différents cas, l'équation peut être différente. Par conséquent, comprenez-le bien pour pouvoir le mémoriser par cœur.
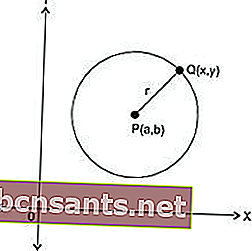
Le cercle est un ensemble de points équidistants d'un point. Les coordonnées de ces points sont déterminées par la disposition des équations. Ceci est déterminé en fonction de la longueur du rayon et des coordonnées du centre du cercle.
Équations de cercle
Il existe différents types d'équations, à savoir des équations formées à partir du point central et du rayon et une équation que l'on peut trouver pour le point central et le rayon.
Équation générale du cercle
Il existe une équation générale, comme ci-dessous:
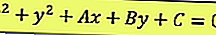
À en juger par l'équation ci-dessus, le point central et le rayon peuvent être déterminés, sont:
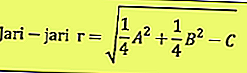
Le centre du cercle est:
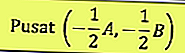
Au centre de P (a, b) et du rayon r
À partir d'un cercle, si vous connaissez le point central et le rayon, vous obtiendrez la formule:
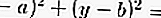
Si vous connaissez le centre d'un cercle et le rayon du cercle où (a, b) est le centre et r est le rayon du cercle.
À partir de l'équation obtenue ci-dessus, nous pouvons déterminer si le point inclus est situé sur le cercle, à l'intérieur ou à l'extérieur. Pour déterminer l'emplacement du point, en utilisant la substitution de points dans les variables x et y, puis en comparant les résultats avec le carré du rayon du cercle.
Un point M (x 1 , y 1 ) est:
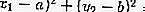
Sur le cercle:
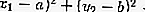
À l'intérieur du cercle:
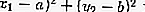
En dehors du cercle:
At avec centre O (0,0) et rayon r
Si le point central est à O (0,0), alors faites la substitution dans la partie précédente, à savoir:
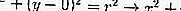
À partir de l'équation ci-dessus, il peut être déterminé l'emplacement d'un point sur le cercle.
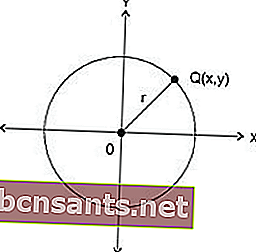
Un point M (x 1 , y 1 ) est:
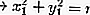
Sur le cercle:
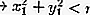
À l'intérieur du cercle:
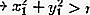
En dehors du cercle: lire aussi: L'art est: définition, fonction, types et exemples [COMPLET]
La forme générale de l'équation peut être exprimée sous les formes suivantes.
(x - a) 2 + (y - b) 2 = r2, ou
X2 + y2 - 2ax - 2by + a2 + b2 - r2 = 0, ou
X2 + y2 + Px + Qy + S = 0, où P = -2a, Q = -2b et S = a2 + b2 - r2
L'intersection des lignes et des cercles
Un cercle avec l'équation x2 + y2 + Ax + By + C = 0 peut être déterminé si une ligne h avec l'équation y = mx + n ne la touche pas, ne l'offense pas ou ne la coupe pas en utilisant le principe discriminant.
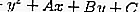
……. (équation 1)
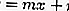
…… .. (équation 2)
En remplaçant l'équation 2 par l'équation 1, vous obtiendrez une équation quadratique, à savoir:
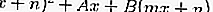
A partir de l'équation quadratique ci-dessus, en comparant les valeurs discriminantes, on peut voir si la ligne n'offense / coupe pas, n'offense ou ne coupe pas le cercle.
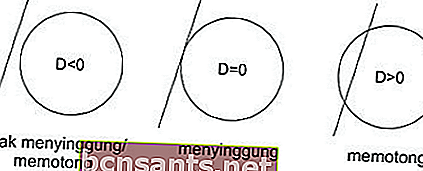
La ligne h ne coupe pas / n'offense pas le cercle, donc D <0
La ligne h est tangente au cercle, donc D = 0
La ligne h coupe le cercle, donc D> 0
Équations des tangentes aux cercles
1. Équation des tangentes passant par un point sur un cercle
Les tangentes à un cercle rencontrent exactement un point situé sur le cercle. A partir du point d'intersection de la tangente et du cercle, l'équation de la droite de la tangente peut être déterminée.
L'équation de la tangente au cercle passant par le point P (x 1 , y 1 ), peut être déterminée, à savoir:
- Forme
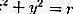
L'équation de la tangente
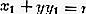
- Forme
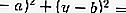
L'équation de la tangente
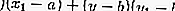
- Forme
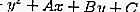
L'équation de la tangente
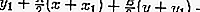
Exemple de problèmes:
L'équation de la tangente passant par le point (-1,1) sur le cercle
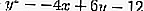
sont:
Répondre:
Connaître l'équation du cercle
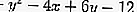
où A = -4, B = 6 et C = -12 et x 1 = -1, y 1 = 1
PGS est
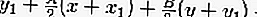
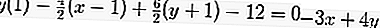
Donc l'équation de la tangente est
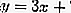
2. L'équation tangente au dégradé
Si une droite de pente m est tangente à un cercle,
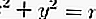
alors l'équation de la tangente est:
Si c'est un cercle,
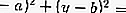
puis l'équation de la tangente:

Si c'est un cercle,
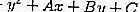
puis l'équation de la tangente en substituant r par,
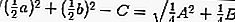
pour que:
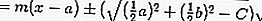
ou
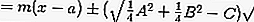
3. Equations des tangentes aux points extérieurs au cercle
À partir d'un point extérieur au cercle, deux tangentes au cercle peuvent être dessinées.
Lire aussi: Démocratie: définition, histoire et types [COMPLET]Pour trouver l'équation tangente, la formule d'équation de ligne régulière est utilisée, à savoir:
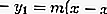
Cependant, à partir de cette formule, la valeur de la pente de la droite est inconnue. Pour trouver la pente de la ligne, remplacez l'équation par l'équation du cercle par l'équation. Puisque la droite est une tangente, alors à partir de l'équation, la substitution résulte de la valeur D = 0, et la valeur de m sera obtenue
Exemple de problèmes
Exemple de problème 1
Un cercle a un point central (2, 3) et mesure 8 cm de diamètre. L'équation du cercle est ...
Discussion:
Comme d = 8 signifie r = 8/2 = 4, l'équation du cercle formé est
(x - 2) ² + (y - 3) ² = 42
x² - 4x + 4 + y² -6y + 9 = 16
x² + y² - 4x - 6y - 3 = 0
Exemple de problème 2
Déterminez l'équation générale du cercle centré au point (5,1) et offensant la droite 3 x - 4 y + 4 = 0!
Discussion:
Si vous savez que le centre du cercle ( a , b ) = (5,1) et la tangente au cercle est 3 x - 4 y + 4 = 0, alors le rayon du cercle est formulé comme suit.
Ainsi, l'équation générale du cercle est la suivante.
Ainsi, l'équation générale pour un cercle centré en (5,1) et offensant la droite 3 x - 4 y + 4 = 0 est
Exemple de problème 3
Trouvez l'équation générale d'un cercle centré en (-3,4) et offensant l'axe Y!
Discussion:
Tout d'abord, dessinons d'abord le graphique du cercle, qui est centré en (-3,4) et qui heurte l'axe Y!
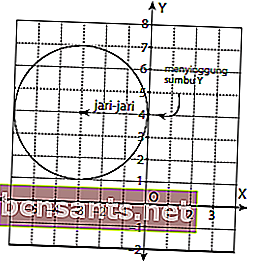
Sur la base de l'image ci-dessus, on peut voir que le centre du cercle est à la coordonnée (-3,4) avec un rayon de 3, de sorte que:
Ainsi, l'équation générale qui est centrée sur (-3,4) et qui offense l'axe Y est
Dans certains cas, le rayon du cercle n'est pas connu, mais la tangente est connue. Alors, comment déterminer le rayon du cercle? Regardez l'image suivante.
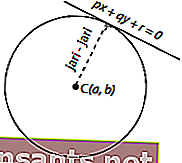
L'image ci-dessus montre que la tangente à l'équation px + qy + r = 0 appartient au cercle centré en C ( a, b ). Le rayon peut être déterminé par l'équation suivante. a, b ). Le rayon peut être déterminé par l'équation suivante.

Peut être utile.
