
L'intégrale indéfinie ou également appelée anti-dérivée est une forme d'opération d'intégration qui produit une nouvelle fonction .
Integral joue un rôle très important en mathématiques. La théorie peut déterminer l'aire sous la courbe d'une fonction.
Integral est utile pour la limite de somme qui est continue sur une fonction continue. Integral est anti-dérivé. Alors, si f est une fonction continue, alors le résultat intégral de la fonction f est noté F.
Les types intégrés basés sur certaines limites fonctionnelles ne sont pas certains. Ce qui suit est une discussion pour les types d'intégrales avec des limites indéfinies.
Intégrale indéfinie
Une intégrale indéfinie ou également connue sous le nom d'anti-dérivé ou d'antidiverentiel est une forme d'opération d'intégration qui produit une nouvelle fonction.
Considérez l'équation suivante.

avec C une constante. La formule intégrale indéfinie est la suivante
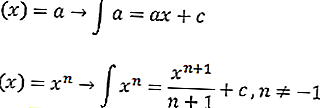
ou égal à

avec
- a (x) ^ n = Fonction d'équation
- a = constante
- x = variable
- n = Puissance de la fonction d'équation
- C = constante
Le résultat de cette intégrale indéfinie est une fonction qui est une nouvelle fonction qui n'a pas de valeur certaine ou définie car il y a encore des variables dans la nouvelle fonction.
Afin que vous puissiez mieux comprendre le concept d'intégrale indéterminée, considérez l'exemple de problème ci-dessous.

Sur la base de cet exemple, une opération intégrale peut être formulée, à savoir
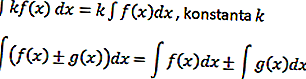
Intégrale trigonométrique
L'intégrale d'une fonction n'est pas nécessairement une constante, linéaire ou polynomiale. Dans cette solution intergalienne, il s'agit souvent d'éléments trigonométriques.
Dans la fonction trigonomique, la définition des intégrales qui est disposée dans le tableau suivant s'applique également.
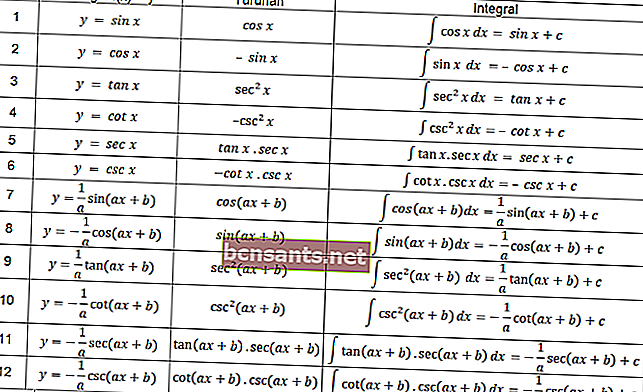
Vous pouvez utiliser les équations du tableau ci-dessus pour résoudre le problème intégral impliquant la trigonométrie.
Pour mieux comprendre les intégrales trigonométriques, vous pouvez comprendre les exemples suivants
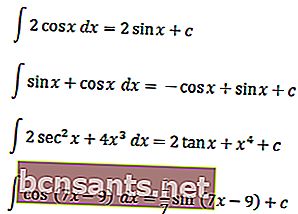
C'était l'explication des intégrales indéterminées dans les fonctions trigonométriques ordinaires et spéciales. Espérons que cela puisse être bien étudié.
Lisez aussi: Les normes de décence: définition, but, sanctions et exemples [COMPLET]Afin de mieux comprendre le concept de cette intégrale, vous pouvez vous entraîner à faire des questions pratiques. Si vous souhaitez demander quelque chose, notez-le dans la colonne des commentaires.
