
La fonction de composition est la combinaison d'une opération de deux types de fonctions f (x) et g (x) afin qu'elle puisse produire une nouvelle fonction.
Formules de fonction de composition
Le symbole de l'opération de la fonction de composition est avec «o», alors il peut être lu composition ou cercle. Cette nouvelle fonction peut être formée à partir de f (x) et g (x), à savoir:
- (brouillard) (x) ce qui signifie que g est entré dans f
- (gof) (x) ce qui signifie que f est mis dans g
Dans la composition, la fonction est également appelée fonction unique.
Qu'est-ce qu'une fonction unique?
Une fonction unique est une fonction qui peut être désignée par les lettres «fog» ou peut être lue «f roundabout g». La fonction "brouillard" est la fonction g qui se fait d'abord puis suivie de f.
Pendant ce temps, pour la fonction "gof", la fonction g arrondit f. Ainsi, "gof" est une fonction où f est fait en premier au lieu de g.
Alors la fonction (fog) (x) = f (g (x)) → la fonction g (x) se compose comme une fonction f (x)
Afin de comprendre cette fonction, considérez l'image ci-dessous:
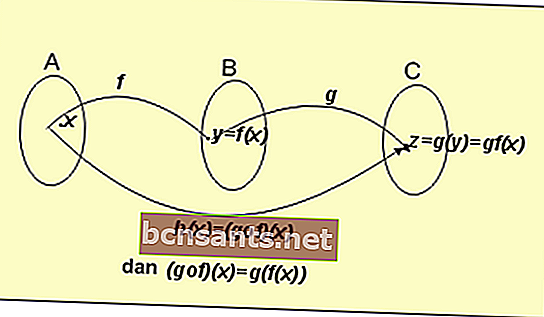
À partir du schéma de formule ci-dessus, la définition que nous avons obtenue est:
Si f: A → B est déterminé par la formule y = f (x)
Si g: B → C est déterminé par la formule y = g (x)
Ensuite, nous obtenons un résultat des fonctions g et f:
h (x) = (gof) (x) = g (f (x))
À partir de la définition ci-dessus, nous pouvons conclure que les fonctions impliquant les fonctions f et g peuvent être écrites:
- (gof) (x) = g (f (x))
- (brouillard) (x) = f (g (x))
Propriétés de la fonction de composition
Il existe plusieurs propriétés de la fonction de composition qui sont décrites ci-dessous.
Si f: A → B, g: B → C, h: C → D, alors:
- (brouillard) (x) ≠ (gof) (x). La nature commutative ne s'applique pas
- [fo (goh) (x)] = [(brouillard) oh (x)]. est associatif
- Si la fonction d'identité est I (x), alors (fol) (x) = (lof) (x) = f (x)
Exemple de problèmes
Problème 1
Étant donné deux fonctions, chacune f (x) et g (x), respectivement, à savoir:
f (x) = 3x + 2
g (x) = 2 - x
Déterminer:
a) ( f o g ) (x)
b) ( g o f ) (x)
Répondre
Connu:
f (x) = 3x + 2
g (x) = 2 - x
( f o g ) (x)
"Branchez g (x) dans f (x)"
être:
( f o g ) (x) = f ( g (x))
= f (2 - x)
= 3 (2 - x) + 2
= 6 - 3x + 2
= - 3x + 8
( g o f ) (x)
"Branchez le f (x) dans g (x)"
Jusqu'à ce qu'il devienne:
( f o g ) (x) = g ( f (x))
= g (3x + 2)
= 2 - (3x + 2)
= 2 - 3x - 2
= - 3x
Problème 2
Si l'on sait que f (x) = 3x + 4 et g (x) = 3x quelle est la valeur de (fog) (2).
Répondre:
(brouillard) (x) = f (g (x))
= 3 (3x) + 4
= 9x + 4
(brouillard) (2) = 9 (2) + 4
= 22
Problème 3
Étant donné la fonction f (x) = 3x - 1 et g (x) = 2 × 2 + 3. La valeur de la composition de la fonction ( g o f ) (1) =….?
Répondre
Connu:
f (x) = 3x - 1 et g (x) = 2 × 2 + 3
( g o f ) (1) =…?
Branchez f (x) dans g (x) puis remplissez avec 1
( g o f ) (x) = 2 (3 x - 1) 2 + 3
( g o f ) (x) = 2 (9 x 2 - 6x + 1) + 3
( g o f ) (x) = 18x 2 - 12x + 2 + 3
( g o f ) (x) = 18 × 2 - 12x + 5
( g o f ) (1) = 18 (1) 2 - 12 (1) + 5 = 11
Problème 4
Il a deux fonctions:
f (x) = 2x - 3
g (x) = x2 + 2x + 3
Si (brouillard) (a) vaut 33, trouvez la valeur de 5a
Répondre:
Rechercher d'abord (brouillard) (x)
(brouillard) (x) vaut 2 (x2 + 2x + 3) - 3
(brouillard) (x) est égal à 2 × 2 4x + 6 - 3
(brouillard) (x) est égal à 2 × 2 4x + 3
33 est identique à 2a2 4a + 3
2a2 4a - 30 vaut 0
a2 + 2a - 15 vaut 0
Lisez aussi: Formules commerciales: explication du matériel, exemples de questions et discussionFacteur:
(a + 5) (a - 3) vaut 0
a = - 5 ou a égal à 3
À
5a = 5 (−5) = −25 ou 5a = 5 (3) = 15
Problème 5
Si (brouillard) (x) = x² + 3x + 4 et g (x) = 4x - 5. Quelle est la valeur de f (3)?
Répondre:
(brouillard) (x) vaut x² + 3x + 4
f (g (x)) vaut x² + 3x + 4
g (x) est égal à 3 Donc,
4x - 5 vaut 3
4x est égal à 8
x est égal à 2
f (g (x)) = x² + 3x + 4 et pour g (x) égal à 3 on obtient x égal à 2
Jusqu'à: f (3) = 2² + 3. 2 + 4 = 4 + 6 + 4 = 14
Ainsi, l'explication concernant la formule de la fonction de composition est un exemple du problème. Peut être utile.
