
Le tableau trigonométrique sin cos tan est une série de tableaux contenant la valeur trigonométrique ou sin cos tangente d'un angle.
Dans cet article, un tableau des valeurs trigonométriques pour sin cos tan est présenté sous différents angles spéciaux allant de 0 ° à 360 ° (ou ce que l'on appelle communément l'angle de cercle à 360 degrés), afin que vous n'ayez plus à vous soucier de les mémoriser.
Quant à la formule d'identité trigonométrique, vous pouvez la lire dans cet article.
Définition de Sin Cos Tan
Avant d'entrer dans le tableau des valeurs trigonométriques, cela nous aide à comprendre d'abord les termes trigonométrie et sin cos tan.
- La trigonométrie est une branche des mathématiques qui étudie la relation entre la longueur et l'angle d'un triangle.
- Sin (sinus) est le rapport de la longueur dans un triangle entre l'avant de l'angle et l'hypoténuse, y / z.
- Cos (cosinus) est le rapport de la longueur dans un triangle entre le côté de l'angle et l'hypoténuse, x / z.
- Tan (tangente) est le rapport des longueurs dans un triangle entre l'avant du coin et le côté, y / x.

Toutes les comparaisons trigonométriques tan sin cos sont limitées à valides uniquement pour les triangles rectangles ou triangles avec un angle de 90 degrés.
Tableau de trigonométrie à angle spécial du quadrant I (0 à 90 degrés)
| Coin | 0 º | 30 º | 45 º | 60 º | 90 º |
| Péché | 0 | 1/2 | 1/2 √2 | 1/2 √3 | 1 |
| Cos | 1 | 1/2 √3 | 1/2 √2 | 1/2 | 0 |
| bronzer | 0 | 1/2 √3 | 1 | √3 | ∞ |
Tableau de trigonométrie du quadrant d'angle spécial II (90-180 degrés)
| Coin | 90 º | 120 º | 135 º | 150 º | 180 º |
| Péché | 1 | 1/2 √3 | 1/2 √2 | 1/2 | 0 |
| Cos | 0 | - 1/2 | - 1/2 √2 | - 1/2 √3 | -1 |
| bronzer | ∞ | -√3 | -1 | - 1/3 √3 | 0 |
Sin Cos Tan Table Special Angle Quadrant III (180-270 degrés)
| Coin | 180 º | 210 º | 225 º | 240 º | 270 º |
| Péché | 0 | - 1/2 | - 1/2 √2 | - 1 / 2√3 | -1 |
| Cos | -1 | - 1 / 2√3 | - 1 / 2√2 | - 1/2 | 0 |
| bronzer | 0 | 1 / 3√3 | 1 | √3 | ∞ |
Cos Sin Tan Table Special Angle Quadrant IV (270-360 degrés)
| Coin | 270 º | 300 º | 315 º | 330 º | 360 º |
| Péché | -1 | -½√3 | -½√2 | -½ | 0 |
| Cos | 0 | ½ | ½√2 | ½√3 | 1 |
| bronzer | ∞ | -√3 | -1 | -1 / 3√3 | 0 |
Ceci est une liste complète des tableaux trigonométriques de tous les angles spéciaux de 0 à 360 degrés.
Lisez aussi: Processus du mécanisme de vision humaine et conseils de soins oculairesVous pouvez utiliser ce tableau pour faciliter le calcul ou l'analyse de la trigonométrie en mathématiques.
Rappel de la table trigonométrique d'angle spécial sans mémorisation
En fait, vous n'avez pas à vous soucier de mémoriser toutes les valeurs trigonométriques sous tous les angles.
Tout ce dont vous avez besoin est un concept de compréhension de base que vous pouvez utiliser pour connaître la valeur de déclenchement d'un angle particulier.
Il vous suffit de vous souvenir des composantes de la longueur des côtés du triangle à des angles spéciaux de 0, 30, 45, 60 et 90 degrés.
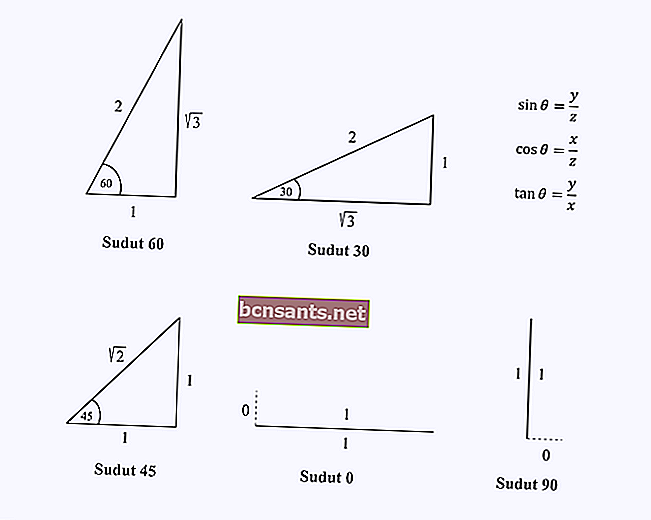
Supposons que vous vouliez trouver la valeur de cos (60).
Il vous suffit de vous souvenir de la longueur du côté du triangle avec un angle de 60 degrés, puis d'effectuer l'opération cosinus, qui est x / z sur ce triangle.
Sur la figure, vous verrez que la valeur de cos 60 = 1/2.
Facile non?
Pour les angles dans les autres quadrants, la méthode est la même et il suffit d'ajuster le signe positif ou négatif de chaque quadrant.
Table en forme de cercle
Si le tableau cos sin tan ci-dessus est trop long à retenir, même si la méthode du concept d'angle spécial que vous pensez est encore difficile ...
Vous pouvez utiliser le tableau trigonométrique sous la forme d'un cercle pour voir directement la valeur de sin cos tan sous un angle de 360 degrés.
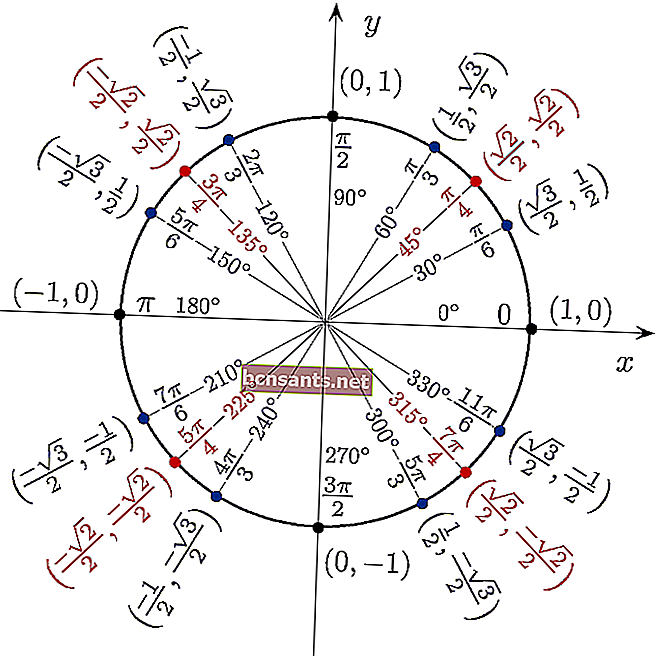
Astuces rapides pour mémoriser les tableaux trigonométriques
En plus des méthodes ci-dessus, il existe une autre méthode que vous pouvez utiliser pour vous souvenir facilement des tables de formules trigonométriques.
Les étapes à suivre sont les suivantes:
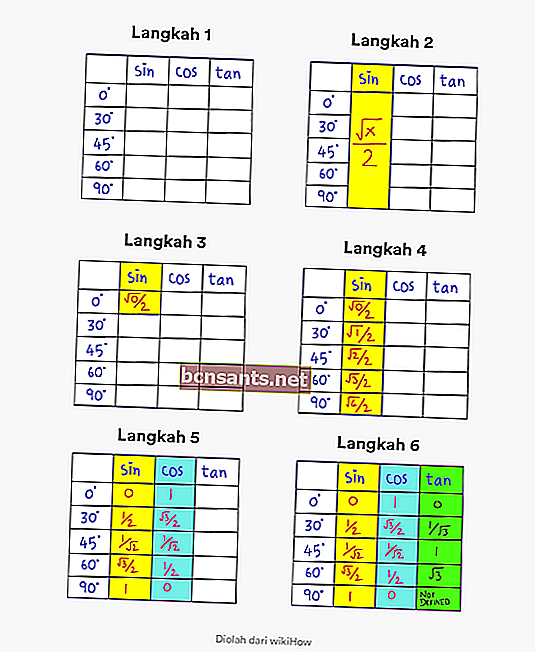
- Étape 1 . Créez un tableau contenant des angles de 0 à 90 degrés et des colonnes avec la description sin cos tan
- Étape 2 . Notez que la formule générale du péché à un angle de 0 à 90 degrés est √x / 2.
- Étape 3 . Remplacez la valeur x par 0 sur √x / 2 dans la toute première colonne. Coin supérieur gauche.
- Étape 4. Remplissez la séquence en changeant le x en 0, 1, 2, 3, 4 dans la colonne sin. Ainsi vous avez obtenu la valeur trigonométrique complète sin
- Étape 5 . Pour trouver la valeur de cos, tout ce que vous avez à faire est d'inverser l'ordre dans la colonne sin.
- Étape 6 . Pour trouver la valeur de tan, tout ce que vous avez à faire est de diviser la valeur sin par la valeur cos.
Lequel est le plus facile à comprendre pour vous pour vous souvenir de la valeur trigonométrique de tan sin cos?
Dans tous les cas, choisissez celui qui est le plus facile à comprendre pour vous. Parce que chaque personne a un style d'apprentissage différent.
Tableaux pour tous les angles
Si dans les tableaux ci-dessus, les valeurs indiquées ne sont que les valeurs trigonométriques d'angles spéciaux, alors ce tableau montre toutes les valeurs trigonométriques de tous les angles de 0 à 90 degrés.
| Coin | Radians | Péché | Cos | bronzer |
| 0 ° | 0 | 0 | 1 | 0 |
| 1 ° | 0,01746 | 0,01746 | 0,99985 | 0,01746 |
| 2 ° | 0,03492 | 0,03491 | 0,99939 | 0,03494 |
| 3 ° | 0,05238 | 0,05236 | 0,99863 | 0,05243 |
| 4 ° | 0,06984 | 0,06979 | 0,99756 | 0,06996 |
| 5 ° | 0,0873 | 0,08719 | 0,99619 | 0,08752 |
| 6 ° | 0,10476 | 0,10457 | 0,99452 | 0,10515 |
| 7 ° | 0,12222 | 0,12192 | 0,99254 | 0,12283 |
| 8 ° | 0,13968 | 0,13923 | 0,99026 | 0,1406 |
| 9 ° | 0,15714 | 0,1565 | 0,98768 | 0,15845 |
| 10 ° | 0,1746 | 0,17372 | 0,9848 | 0,1764 |
| 11 ° | 0,19206 | 0,19089 | 0,98161 | 0,19446 |
| 12 ° | 0,20952 | 0,20799 | 0,97813 | 0,21265 |
| 13 ° | 0,22698 | 0,22504 | 0,97435 | 0,23096 |
| 14 ° | 0,24444 | 0,24202 | 0,97027 | 0,24943 |
| 15 ° | 0,26191 | 0,25892 | 0,9659 | 0,26806 |
| 16 ° | 0,27937 | 0,27575 | 0,96123 | 0,28687 |
| 17 ° | 0,29683 | 0,29249 | 0,95627 | 0,30586 |
| 18 ° | 0,31429 | 0,30914 | 0,95102 | 0,32506 |
| 19 ° | 0,33175 | 0,32569 | 0,94548 | 0,34448 |
| 20 ° | 0,34921 | 0,34215 | 0,93965 | 0,36413 |
| 21 ° | 0,36667 | 0,35851 | 0,93353 | 0,38403 |
| 22 ° | 0,38413 | 0,37475 | 0,92713 | 0,40421 |
| 23 ° | 0,40159 | 0,39088 | 0,92044 | 0,42467 |
| 24 ° | 0,41905 | 0,40689 | 0,91348 | 0,44543 |
| 25 ° | 0,43651 | 0,42278 | 0,90623 | 0,46652 |
| 26 ° | 0,45397 | 0,43854 | 0,89871 | 0,48796 |
| 27 ° | 0,47143 | 0,45416 | 0,89092 | 0,50976 |
| 28 ° | 0,48889 | 0,46965 | 0,88286 | 0,53196 |
| 29 ° | 0,50635 | 0,48499 | 0,87452 | 0,55458 |
| 30 ° | 0,52381 | 0,50018 | 0,86592 | 0,57763 |
| 31 ° | 0,54127 | 0,51523 | 0,85706 | 0,60116 |
| 32 ° | 0,55873 | 0,53011 | 0,84793 | 0,62518 |
| 33 ° | 0,57619 | 0,54483 | 0,83854 | 0,64974 |
| 34 ° | 0,59365 | 0,55939 | 0,8289 | 0,67486 |
| 35 ° | 0,61111 | 0,57378 | 0,81901 | 0,70057 |
| 36 ° | 0,62857 | 0,58799 | 0.80887 | 0,72693 |
| 37 ° | 0,64603 | 0,60202 | 0,79848 | 0,75396 |
| 38 ° | 0,66349 | 0,61587 | 0,78785 | 0,78172 |
| 39 ° | 0,68095 | 0,62953 | 0,77697 | 0,81024 |
| 40 ° | 0,69841 | 0,643 | 0,76586 | 0,83958 |
| 41 ° | 0,71587 | 0,65628 | 0,75452 | 0,86979 |
| 42 ° | 0,73333 | 0,66935 | 0,74295 | 0,90094 |
| 43 ° | 0,75079 | 0,68222 | 0,73115 | 0,93308 |
| 44 ° | 0,76825 | 0,69488 | 0,71913 | 0,96629 |
| 45 ° | 0,78571 | 0,70733 | 0,70688 | 1 00063 |
| 46 ° | 0.80318 | 0,71956 | 0,69443 | 1,0362 |
| 47 ° | 0,82064 | 0,73158 | 0,68176 | 1.07308 |
| 48 ° | 0,8381 | 0,74337 | 0,66888 | 1.11137 |
| 49 ° | 0,85556 | 0,75494 | 0,6558 | 1,15117 |
| 50 ° | 0,87302 | 0,76627 | 0,64252 | 1,1926 |
| 51 ° | 0,89048 | 0,77737 | 0,62904 | 1 2358 |
| 52 ° | 0,90794 | 0,78824 | 0,61537 | 1.28091 |
| 53 ° | 0,9254 | 0,79886 | 0,60152 | 1,32807 |
| 54 ° | 0,94286 | 0.80924 | 0,58748 | 1,37748 |
| 55 ° | 0,96032 | 0,81937 | 0,57326 | 1,42932 |
| 56 ° | 0,97778 | 0,82926 | 0,55887 | 1,48382 |
| 57 ° | 0.99524 | 0,83889 | 0,5443 | 1,54122 |
| 58 ° | 1,0127 | 0,84826 | 0,52957 | 1,60179 |
| 59 ° | 1.03016 | 0,85738 | 0,51468 | 1,66584 |
| 60 ° | 1,04762 | 0,86624 | 0,49964 | 1 73374 |
| 61 ° | 1,06508 | 0,87483 | 0,48444 | 1,80587 |
| 62 ° | 1,08254 | 0,88315 | 0,46909 | 1,8827 |
| 63 ° | 1.1 | 0,89121 | 0,4536 | 1 96476 |
| 64 ° | 1.11746 | 0,89899 | 0,43797 | 2,05265 |
| 65 ° | 1.13492 | 0,9065 | 0,4222 | 2,14707 |
| 66 ° | 1,15238 | 0,91373 | 0,40631 | 2,24884 |
| 67 ° | 1,16984 | 0,92069 | 0,3903 | 2,35894 |
| 68 ° | 1,1873 | 0,92736 | 0,37416 | 2,4785 |
| 69 ° | 1,20476 | 0,93375 | 0,35792 | 2.60887 |
| 70 ° | 1.22222 | 0,93986 | 0,34156 | 2,75169 |
| 71 ° | 1,23968 | 0,94568 | 0,3251 | 2,90892 |
| 72 ° | 1,25714 | 0,95121 | 0,30854 | 3,08299 |
| 73 ° | 1,2746 | 0,95646 | 0,29188 | 3,27686 |
| 74 ° | 1.29206 | 0,96141 | 0,27514 | 3 49427 |
| 75 ° | 1.30952 | 0,96606 | 0,25831 | 3.73993 |
| 76 ° | 1,32698 | 0,97043 | 0,2414 | 4.01992 |
| 77 ° | 1,34444 | 0,97449 | 0,22442 | 4.34219 |
| 78 ° | 1.36191 | 0,97826 | 0,20738 | 4 71734 |
| 79 ° | 1,37937 | 0,98173 | 0,19026 | 5,15984 |
| 80 ° | 1,39683 | 0,98491 | 0,1731 | 5,68998 |
| 81 ° | 1,41429 | 0,98778 | 0,15587 | 6,33709 |
| 82 ° | 1,43175 | 0,99035 | 0,1386 | 7,14523 |
| 83 ° | 1.44921 | 0,99262 | 0,12129 | 8.18379 |
| 84 ° | 1,46667 | 0,99458 | 0,10394 | 9 56868 |
| 85 ° | 1,48413 | 0,99625 | 0,08656 | 11 5092 |
| 86 ° | 1,50159 | 0,99761 | 0,06915 | 14 4259 |
| 87 ° | 1,51905 | 0,99866 | 0,05173 | 19 3069 |
| 88 ° | 1,53651 | 0,99941 | 0,03428 | 29 153 |
| 89 ° | 1,55397 | 0,99986 | 0,01683 | 59,4189 |
| 90 ° | 1,57143 | 1 | 0 | ∞ |
Espérons que cette explication trigonométrique peut vous être utile.
Ce matériel sera d'une grande utilité pour diverses applications en mathématiques et en physique avancées.
Vous pouvez également apprendre d'autres matériels scolaires à Saintif, tels que les nombres premiers, les conversions d'unités, les formules rectangulaires, etc.
Référence
- Trigonométrie - Wikipédia
- Outils mathématiques - Trigonométrie
