
La formule du triangle pour trouver l'aire de la forme est 1/2 x base x hauteur, pour trouver le périmètre du triangle, vous pouvez trouver la longueur de chaque côté du triangle.
En mathématiques, on nous apprend différentes formes. L'un d'eux est une forme de triangle. La forme du triangle est la forme la plus simple parmi les différents types de formes.
Un triangle est formé de trois côtés avec trois angles délimités par un segment. En outre, l'angle total du triangle est de 180 degrés.
Il existe plusieurs types de triangles. Sur la base de la longueur des côtés, il existe un triangle équilatéral de même longueur de côté, un triangle isocèle avec deux côtés de la même jambe et tout triangle avec trois longueurs de côtés différentes.
Pendant ce temps, sur la base de l'angle, il y a un triangle aigu avec un angle de moins de 90 degrés, un triangle obtus avec un angle de plus de 90 degrés et un triangle rectangle avec un angle de 90 degrés.
En ce qui concerne les triangles, plusieurs composants doivent être connus, notamment l'aire et le périmètre du triangle. Ce qui suit est une explication de l'aire et du périmètre du triangle avec un exemple du problème.
Aire du triangle

L'aire, l'aire ou l'aire est une grandeur qui exprime la taille bidimensionnelle, à savoir une partie de la surface clairement définie par une courbe ou une ligne fermée.
L'aire du triangle correspond à la taille du triangle lui-même. Voici la formule de l'aire d'un triangle:
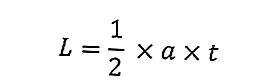
où L est l'aire du triangle (cm 2 ), a est la base du triangle (cm) et h est la hauteur du triangle (cm).
Exemple de problème d'aire d'un triangle
Exemple de problème 1
Il y a un triangle aigu qui a une longueur de base a = 10 cm et a également une hauteur h = 8 cm. Calculez l'aire du triangle.
Lisez aussi: Animaux: caractéristiques, types, exemples [Explication complète]Solution:
Si: a = 10 cm, h = 8 cm
Recherché: L'aire du triangle?
Répondre:
L = ½ xaxt
= ½ x 10 x 8
= 40 cm2
Ainsi, l'aire du triangle aigu est de 40 cm2
Exemple de problème 2
Un triangle rectangle a une base de 15 cm et une hauteur de 20 cm. Trouvez et calculez l'aire du triangle rectangle.
Solution:
Vous savez que: a = 15 cm, h = 20 cm
Recherché: L'aire du triangle?
Répondre:
L = ½ xaxt
= ½ x 15 x 20
= 150 cm2
Ainsi, l'aire du triangle rectangle est de 150 cm2
Exemple de problème 3
Un triangle obtus avec une base de 8 cm et une hauteur de 3 cm, alors quelle est l'aire du triangle?
Solution:
Si: a = 8 cm, h = 3 cm
Recherché: L'aire du triangle?
Répondre:
L = ½ xaxt
= ½ x 8 x 3
= 12 cm2
Ainsi, l'aire du triangle obtus est de 12 cm2
Exemple de problème 4
Un triangle isocèle avec la même longueur de côté est de 13 cm et la base du triangle est de 10 cm. Quelle est l'aire du triangle isocèle?
Solution:
Vous savez: s = 13 cm, a = 10 cm
Recherché: L'aire du triangle?
Répondre:
La hauteur du triangle n'est pas connue, nous utilisons donc la formule de Pythagore pour trouver la hauteur du triangle:

Puisque la hauteur du triangle est connue, alors:
L = ½ xaxt
= ½ x 10 x 12
= 60 cm2
Ainsi, l'aire du triangle isocèle est de 60 cm2
Périmètre du triangle

Le périmètre est le nombre de côtés dans une forme bidimensionnelle. Ainsi, le périmètre du triangle est la somme des côtés du triangle lui-même.
Voici la formule pour le périmètre d'un triangle:
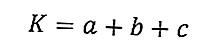
où K est le périmètre du triangle (cm), et a, b, c sont les longueurs des côtés du triangle (cm).
Exemple de périmètre d'un triangle
Exemple de problème 1
Un triangle équilatéral a des côtés de 15 cm de long. Quel est le périmètre du triangle?
Règlement:
Vous savez: longueur du côté = 15 cm
Question posée: circonférence =….?
Répondre:
K = côté a + côté b + côté c
parce que c'est un triangle équilatéral, les longueurs des trois côtés sont égales.
K = 15 + 15 + 15
= 45 cm
Ainsi , le périmètre du triangle équilatéral est de 45 cm
Lisez aussi: L'interaction sociale est - Définition et explication complètesExemple de problème 2
Un triangle arbitraire a des côtés de 3 cm, 5 cm et 8 cm. Calculez le périmètre du triangle.
Règlement:
Vous savez: a = 3 cm, b = 5 cm et c = 8 cm
Question posée: circonférence =….?
Répondre:
K = côté a + côté b + côté c
= 3 + 5 + 8
= 16 cm
Ainsi, le périmètre du triangle est de 16 cm
Exemple de problème 3
Un triangle isocèle a des côtés égaux à 10 cm et une base de 6 cm. Calculez le périmètre du triangle isocèle.
Règlement:
Vous savez que les côtés mesurent 10 cm de long et 6 cm de long
Question posée: circonférence =….?
Répondre:
K = côté a + côté b + côté c
car le triangle est isocèle, alors il y a deux côtés de même longueur, à savoir 10 cm, alors K = 10 + 10 + 6 = 26 cm
Ainsi, le périmètre du triangle isocèle est de 26 cm
Exemple de problème 4
Un triangle isocèle a une hauteur de 8 cm et une base de 12 cm. Calculez le périmètre du triangle.
Règlement:
Vous savez: la hauteur du triangle h = 8 cm
côté de la base a = 12 cm
Question posée : circonférence =….?
Répondre:
K = côté a + côté b + côté c
Les deux côtés du triangle sont inconnus, nous utilisons donc la formule de Pythagore pour trouver la longueur de ce côté.

K = 10 + 10 + 12
K = 32 cm
Ainsi, le périmètre du triangle isocèle est de 32 cm
Ceci est une explication de l'aire d'un triangle et du périmètre du triangle avec des exemples et une discussion. Peut être utile.
