
Si vous parlez de formules, et encore moins de physique, vous serez toujours contacté pour mémoriser des questions. Fondamentalement, la formule n'a pas besoin d'être mémorisée mais elle a juste besoin d'être comprise. Maintenant, je vais vous aider à ne pas mémoriser une formule. Pas du tout de conseils liés au traitement du cerveau pour le mémoriser, pas du tout, mes amis. Alors laissez-moi vous présenter, Dimensions of Magnitude!
Donc, si vous êtes un enfant de la physique, vous serez sûrement familier avec le nom Dimension of Quantity. Vous saurez donc qu'il existe 7 grandeurs principales et leurs unités. Ces sept quantités ont donc aussi leurs dimensions. Vous pouvez donc en voir plus ci-dessous.

Et pour certaines quantités dérivées, les dimensions seront comme ça
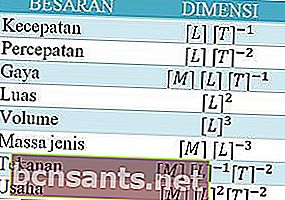
Alors qu'est-ce que cela a à voir avec le fait de ne pas connaître la formule?

Alors je vais vous donner un exemple. Supposons que vous ayez oublié la formule de la période d'un pendule. Ce dont vous vous souvenez, c'est qu'il a une valeur constante de 2 pi et qu'il est lié à la longueur de la corde et à l'accélération due à la gravité et donc vous pensez qu'il semble que la masse du pendule ait un effet. Bon alors commençons.
Tout d'abord, vous listez d'abord les magnitudes affectant la période du pendule et comme mentionné ci-dessus,
- Longueur de corde (l)
- Accélération due à la gravité (g)
- Masse du pendule (m)
Eh bien et maintenant nous faisons la magie. Pour la période elle-même, la quantité est le temps, la longueur de la corde est la longueur et l'accélération due à la gravité qui est une quantité dérivée qui dépend de la longueur et du temps. Ok pour la prochaine, nous pouvons le faire comme ceci:
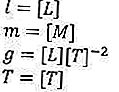
Quoi qu'il en soit, des connaissances de base sur les exposants sont également très nécessaires ici, donc c'est mieux avant de continuer, assurez-vous de maîtriser les exposants et n'oubliez pas l'algèbre bien sûr.
Lisez aussi: La formule du périmètre d'un triangle (explication, exemples de questions et discussion)Maintenant, nous faisons l'équation comme ça
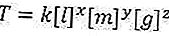
Alors, pourquoi y a-t-il des variables? Oui, parce que nous ne savons toujours pas que la formule va être comme comment, c'est pourquoi nous y donnons une variable. Alors pourquoi pas pour T (point)? Parce que nous savons certainement que pendant cette période, l'unité n'est qu'à quelques secondes d'un rang, et que diriez-vous de cela. Et pour k lui-même, c'est une constante qui n'affectera pas la solution plus tard. D'accord, vous l'aurez compris, alors nous recherchons la valeur de chaque variable
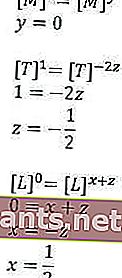
Pour que nous puissions obtenir la formule en substituant les valeurs qui ont été obtenues
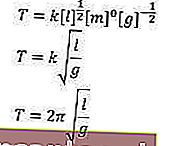
Ouais, nous l'avons bro.

Eh bien, c'est ce qu'on appelle souvent l'analyse dimensionnelle. L'analyse dimensionnelle est très utile pour les scientifiques et ingénieurs existants pour effectuer des calculs précis. Alors restez aux gars!
Ce message est la soumission de l'auteur. Vous pouvez également créer votre propre écriture sur Saintif en rejoignant la Communauté Saintif
Référence:
Giancoli, Douglas. 2014. Principes de physique avec applications 7e éd. New Jersey: PEARSON Prentice Hall
