
La collection suivante de formules mathématiques pour le SD de 6e année comprend:
- Une collection de formules de volume pour l'espace de construction, formule pour l'échelle
- Calcul de la surface plane
- Opérations sur les nombres entiers
- Formules d'opération de comptage de nombres mixtes
- La formule pour FPB et KPK est deux nombres
- Traitement et présentation des données
- Système de coordonnées, formules de volume et de temps
- Addition et soustraction de fractions et détermination de la racine carrée des nombres cubiques.
Formules mathématiques de classe 6 Calculer le volume de construction d'une pièce
| Nom de l'espace de création | Formules de volume |
| Tube | V = phi r² xt |
| Triangle droit Prima | V = aire de la base x hauteur |
Échelle de calcul de la collection de formules mathématiques de classe 6
| Formules d'échelle | = Distance sur l'image (carte) / Distance réelle |
| Formules de distance dans la Fig | = Distance réelle x échelle |
| Formules de distance réelle | = Distance sur l'image (carte) / échelle |
Collection de formules pour calculer l'aire d'un appartement
| Figure à deux dimensions | Formule de surface |
| Construire un carré plat | L = côté x côté = s² |
| Construire un triangle plat | L = ½ base x hauteur |
| Construire un cercle plat | L = phi x r² |
| Construction trapézoïdale | L = ½ t × (a + b) |
| Build Flat Kite - Kite | L = ½ xd 1 xd 2 |
| Construire un parallélogramme plat | L = Base x Hauteur |
| Get Up Flat Rhombus | L = ½ xd 1 xd 2 |
| Construire un rectangle plat | L = longueur x largeur |
Collection de formules d'opération d'entiers SD de classe 6
- Propriétés commutatives de l'addition, formules générales: a + b = b + a
Par exemple: 2 + 4 = 4 + 2 = 6 ou 5 + 10 = 10 + 5 = 15
- Nature commutative de la multiplication, formules générales: axb = bxa
Par exemple: 3 x 5 = 5 x 3 = 15 ou 10 x 2 = 2 x 10 = 20
- Propriétés distributives de la multiplication à l'addition
Formule générale: ax (b + c) = (axb) + (axc)
Exemple :
| 2 x (5 + 10) | = 2 x 5 + 2 x 10 |
| = 10 + 20 | |
| = 30 |
- Nature distributive de la multiplication à la soustraction
Formule générale: ax (b - c) = (axb) - (axc)
Exemple :
| 2 x (10 à 5) | = 2 x 10 - 2 x 5 |
| = 20 + 10 | |
| = 10 |
Collection de formules d' opérations de calcul de nombres mixtes
L'opération de calcul de nombres mixtes comporte 2 conditions, à savoir, entre autres:
Lisez aussi: Caractéristiques des planètes du système solaire (COMPLET) avec images et explicationsPremièrement, s'il y a des crochets (), faites d'abord ce qui se trouve à l'intérieur des crochets.
Deuxièmement, s'il n'y a pas de crochets (), faites d'abord Multiplication & Division, puis Addition & Soustraction.
Exemple:
| = 7000 - 40 x 100: 4 + 200 | = 1000: 10 x 2 - (200 + 50) | |
| = 7 000 - 1 000 + 200 | = 1000: 10 x 2 à 150 | |
| = 6200 | Ou | = 100 x 2 - 150 |
| = 200 - 150 | ||
| = 50 |
La formule pour FPB et KPK est deux nombres
Comment déterminer le FPB (plus grand facteur commun) Deux nombres, entre autres, Trouvez le facteur dans chacun de ces nombres, déterminez le facteur commun des deux nombres et multipliez le facteur commun (même facteur) qui a la plus petite puissance.
Exemple :
| 27 | = 3³ |
| 18 | = 2 x 3² |
Le facteur commun pour le FPB de deux nombres est 3, et la puissance la plus basse est 3² = 9
Comment déterminer le LCM (le plus petit commun multiple) pour deux nombres, entre autres, trouver le facteur premier de chacun de ces nombres, multiplier tous les facteurs et facteurs qui sont les mêmes, selon le rang le plus élevé.
Par exemple: valeurs KPK 12 et 15
| 12 | = 2² x 3 |
| 15 | = 3 x 5 |
Valeur LCM Deux nombres ci-dessus: 2² x 3 x 5 = 50
Traitement et présentation des données
Le mode est la valeur qui apparaît le plus.
La valeur minimale est la valeur la plus petite et la plus basse de toutes les données.
La valeur maximale est la valeur la plus élevée de toutes les données qu'il contient.
La moyenne est pour la moyenne est recherchée en additionnant tous les échantillons divisés par le nombre d'échantillons.
- Recherche du système de coordonnées
- L'axe des x est également appelé absis (x) et l'axe des y est également appelé ordonnée (y).
- Un plan de coordonnées cartésien sera formé par 2 axes, à savoir l'axe vertical (axe y) et l'axe horizontal (axe x).
- À partir du point zéro, l'axe vertical sera vers le haut et l'axe horizontal sera vers la droite qui a une valeur positive.
- À partir du point zéro, l'axe vertical descendra et l'axe horizontal ira vers la gauche qui a une valeur négative.
- La recherche des coordonnées d'un objet peut être trouvée en trouvant l'emplacement sur l'axe x à droite ou à gauche avec la position sur l'axe y vers le haut ou vers le bas.
Relation d'unité de volume
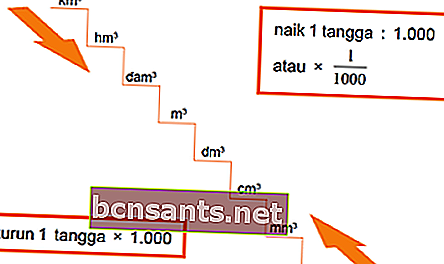
Exemple:
1 km3 = 1000 hm3 (en bas d'une échelle)
1 m3 = 1000000 cm3 (en bas de 2 marches)
1 m3 = 1/1 000 dam3 (1 échelle)
1 m3 = 1/1 000 000 hm3 (monter 2 marches)
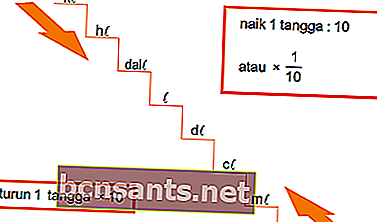
Volume en litres
Unité de temps
| Une minute | = 60 secondes |
| Une heure | = 60 minutes |
| Un jour | = 24 heures |
| Une semaine | = 7 jours |
| Un mois | = 30 jours / 31 jours |
| Un mois | = 4 semaines |
| Un ans | = 52 semaines |
| Un ans | = 12 mois |
| Un Windu | = 8 ans |
| Une décennie | = 10 ans |
| Une décennie | = 10 ans |
| Un siècle | = 100 ans |
| Un millénaire | = 1000 ans |
Conversion de secondes
- 1 minute = 60 secondes
- 1 heure = 3 600
- 1 jour = 86 400
- 1 mois = 2592000 secondes
- 1 an = 31104000 secondes
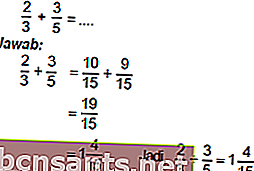
Addition et soustraction de fractions
Pour pouvoir additionner et soustraire des fractions, commencez par égaliser les dénominateurs.
Exemple:
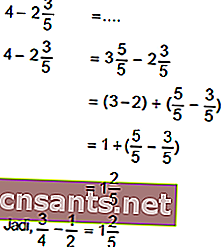
Multiplier et diviser des fractions
La multiplication des fractions est assez facile. Le numérateur multiplié par le numérateur. Le dénominateur multiplié par le dénominateur. Si cela peut être simplifié, simplifiez:

La division fractionnelle équivaut à multiplier par le diviseur de la fraction.
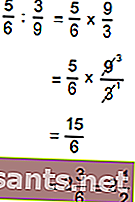
Trouver la racine cubique d'un nombre cubique
13 se lit comme un cube = 1 × 1 × 1 = 1
23 se lit comme deux à la puissance trois = 2 × 2 × 2 = 8
33 se lit comme trois cubes = 3 × 3 × 3 = 27
43 se lit comme quatre à la puissance trois = 4 × 4 × 4 = 64
53 est lu comme cinq à la puissance de trois = 5 × 5 × 5 = 125
1, 8, 27, 64, 125, etc. sont des nombres cubes ou des puissances de 3
Addition et soustraction
23 + 33 = (2 × 2 × 2) + (3 × 3 × 3)
= 8 + 27
= 35
63 - 43 = (6 × 6 × 6) - (4 × 4 × 4)
= 216 - 64
= 152
Multiplication et division
23 × 43 = (2 × 2 × 2) × (4 × 4 × 4)
= 8 × 64
= 512
63: 23 = (6 × 6 × 6): (2 × 2 × 2)
= 216: 8
= 27
Il s'agit d'une collection de formules mathématiques de 6e année élémentaire qui apparaissent souvent dans les questions de l'examen final national (UAN) et de l'examen national (ONU). Peut être utile.
