
La construction d'espace est un sujet qui est souvent discuté en mathématiques, la formule est souvent un problème de mathématiques aux niveaux primaire et secondaire.
L'espace du bâtiment peut être interprété comme un bâtiment qui a mathématiquement du volume ou du contenu. On peut également interpréter que la forme d'un espace est une forme tridimensionnelle qui a du volume ou de l'espace et est limitée par les côtés.
Il existe différentes formes d'espace lui-même, telles que des blocs, des cubes, des tubes, des balles, etc.
Chacune de ces formes a une formule pour le volume et la surface respectivement. Cela rend parfois difficile la mémorisation de nombreux élèves.
Dans ce qui suit, j'ai fait une liste complète des formules de construction, afin que vous puissiez facilement résoudre divers problèmes mathématiques sur ce sujet.
1. Cube
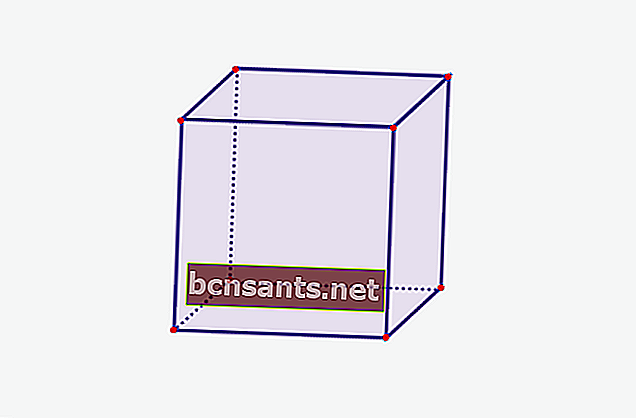
| Volume du cube | V = sxsxs |
| La surface du cube | L = 6 x (sxs) |
| Encerclez le cube | K = 12 xs |
| Zone d'un côté | L = sxs |
2. Poutres
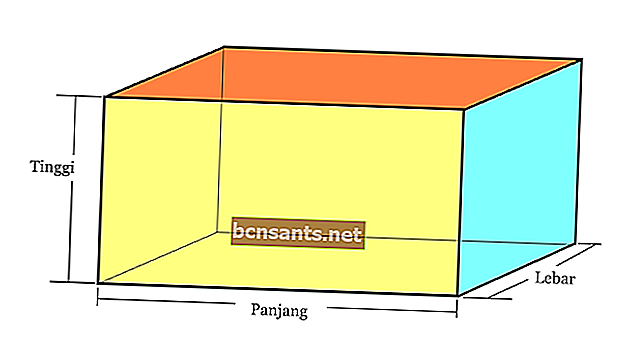
| Bloquer le volume | V = pxlxt |
| Surface de bloc | L = 2 x (pl + lt + pt) |
| Espace diagonal | d = √ ( p2 + l2 + t2) |
| La circonférence de la poutre | K = 4 x (w + l + h) |
3. Prisme triangulaire
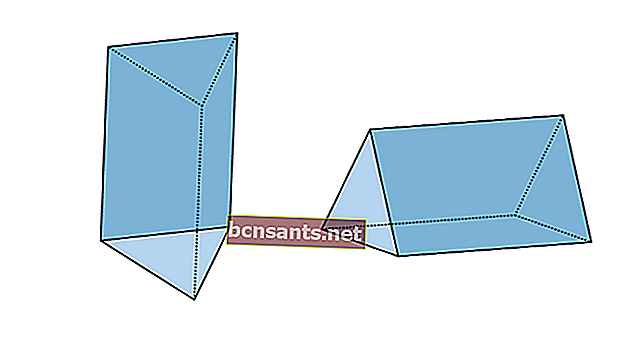
| Le volume du prisme triangulaire | V = aire de la base xt |
| La surface du prisme triangulaire | L = périmètre de la base xt + 2 x aire de la base du triangle |
4. Cinquième quadrilatère
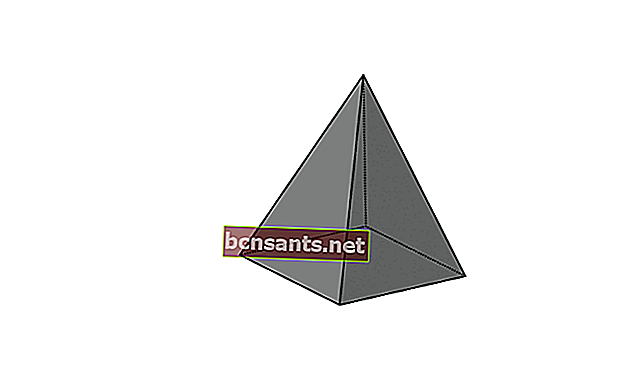
| Le volume de la pyramide | V = 1/3 xpxlxt |
| La superficie de la pyramide | L = aire de la base + aire du boîtier pyramidal |
5. Cinquième triangle
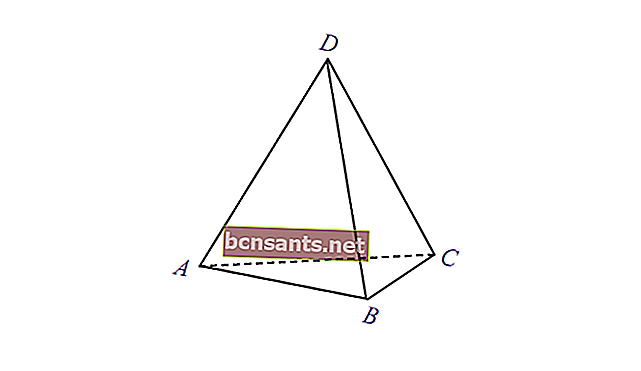
| Le volume de la pyramide | V = 1/3 x aire de la base xt |
| Superficie | L = aire de la base + aire du boîtier pyramidal |
6. Tubes

| Volume du tube | V = π x r2 xt |
| Surface du tube | L = (2 x aire de la base) + (périmètre de la base x hauteur) |
7. Cônes

| Volume du cône | V = 1/3 x π x r2 xt |
| La surface du cône | A = (π x r2) + (π xrxs) |
8 balles

| Volume de balle | V = 4/3 x π x r3 |
| La surface du ballon | A = 4 x π x r2 |
Tableau complet des formules de construction
Vous pouvez également obtenir brièvement la liste ci-dessus en consultant le tableau ci-dessous. Vous pouvez également enregistrer cette image afin de pouvoir la revoir à tout moment.
Ceci est une explication de la formule de forme de bâtiment pour calculer le volume et la surface.
J'espère que l'explication ci-dessus pourra vous aider à comprendre la forme de l'espace, afin que vous puissiez l'utiliser pour résoudre des problèmes de mathématiques et ses diverses applications dans la vie quotidienne.
Référence
- Examen des formules de volume - Khan Academy
- Feuille de formule de géométrie
