Formule du triangle de Pascal et problème d'exemple

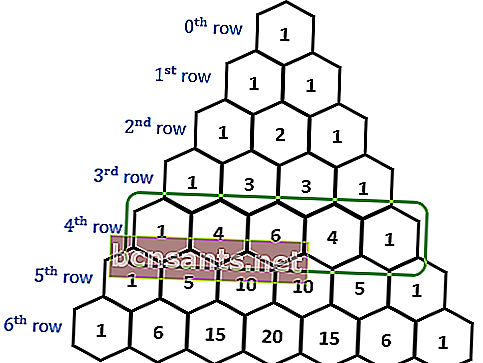
Le triangle de Pascal est un arrangement de triangles créé en additionnant des éléments adjacents dans la ligne précédente. Cet agencement de triangles est réalisé en ajoutant des éléments adjacents dans la rangée précédente.

Supposons que les variables a et b soient additionnées, puis élevées à la puissance de 0 à la puissance de 3, le résultat est la description suivante.

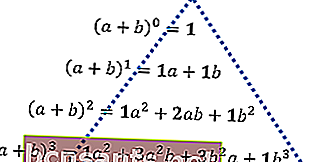
Ensuite, considérez la disposition des nombres en gras de haut en bas, jusqu'à ce que vous trouviez une forme de triangle. Ce modèle numérique est ci-après appelé le triangle de Pascal.

Comprendre le triangle de Pascal

Le triangle de Pascal est la règle géométrique sur le coefficient binomial dans un triangle.

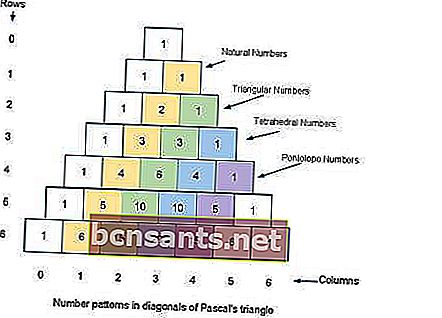
Le triangle porte le nom du mathématicien Blaise Pascal, bien que d'autres mathématiciens l'aient étudié des siècles avant lui en Inde, en Perse, en Chine et en Italie.

Concept de règles

Le concept du triangle de Pascal est un système de calcul pour ce triangle indépendamment des variables a et b. Cela signifie qu'il suffit de faire attention au coefficient binomial, comme suit:

1. Dans la ligne zéro, écrivez uniquement le chiffre 1.
2. Dans chaque ligne ci-dessous, écrivez le chiffre 1 à gauche et à droite.
3. La somme des deux nombres ci-dessus, puis écrite sur la ligne ci-dessous.
4. Le numéro 1 à gauche et à droite selon (2), entoure toujours le résultat (3)
5. Les calculs peuvent être poursuivis avec le même schéma.

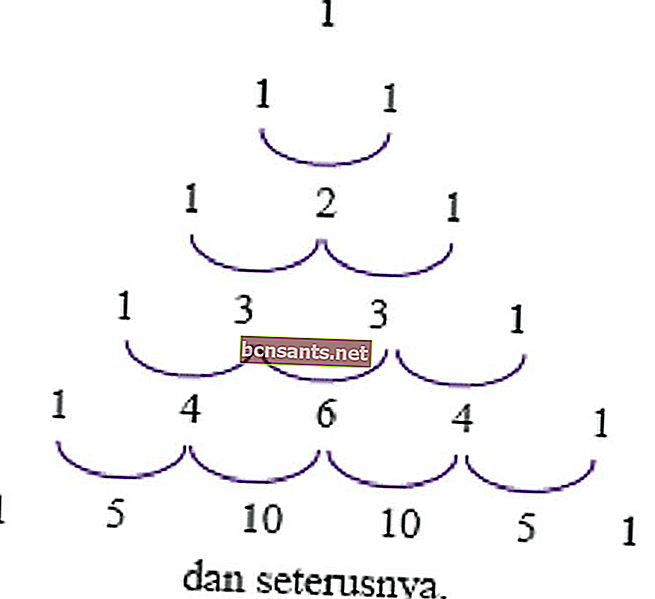
Une utilisation de ce triangle est de déterminer le coefficient de puissance (a + b) ou (ab) pour le rendre plus efficace. Cette utilisation est décrite dans les exemples suivants.

Exemple de problèmes

Indice: faites attention au triangle de Pascal.

1. Quelle est la traduction (a + b) 4?

Solution : pour (a + b) 4

• Tout d'abord, les variables a et b sont arrangées, à partir de a4b ou a4
• Ensuite, la puissance de a tombe à 3, ce qui est a3b1 (le total à la puissance de ab doit être de 4)
• Puis la puissance de a tombe à 2, devenant a2b2
• Puis la puissance de a tombe à 1, devenant ab3
• Puis la puissance de a tombe à 0, à b4
• Ensuite, écrivez l'équation avec le coefficient devant le blanc

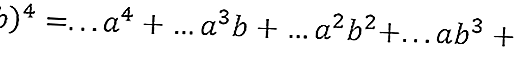
Selon la figure 2 dans le 4ème ordre, les nombres 1,4,6,4,1 sont obtenus, donc la translation (a + b) 4 est obtenue

2. Quel est le coefficient a3b3 en (a + b) 6?

Lisez également: Matériau du champ magnétique: formules, exemples de problèmes et explications

Solution :

Sur la base de la question numéro 1, l'ordre des variables de (a + b) 6 est organisé, à savoir

a6, a5b1, a4b2, a 3 b 3 .

Cela signifie qu'à la quatrième place (image 2, séquence 6) dans le motif 1, 6, 15, 20 est 20 . Ainsi, 20 a3b3 peuvent être écrits.

3. Déterminez la translation de (3a + 2b) 3

Règlement

La formule générale du triangle pascal comme la somme des variables a et b à la puissance 3 est présentée comme suit

En changeant les variables en 3a et 2b, on obtient