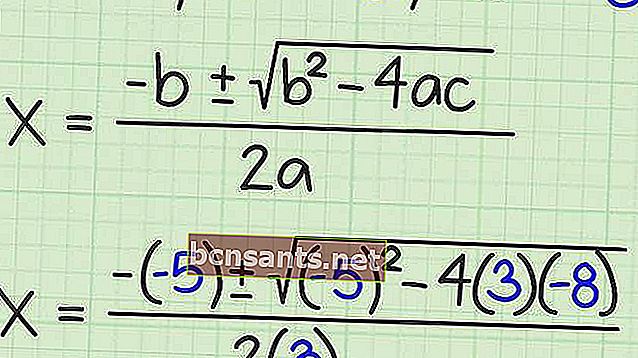
La formule ABC est un excellent moyen de trouver les racines de diverses formes d'équations quadratiques même si le résultat n'est pas un entier.
L'équation quadratique ax2 + bx + c = 0 peut être résolue en utilisant plusieurs méthodes. Parmi eux se trouvent la méthode d'affacturage, complétant le carré ABC et la formule.
Parmi ces méthodes, la formule abc est excellente car elle peut être utilisée pour trouver les racines de diverses formes d'équations quadratiques même si le résultat n'est pas un entier.
Ce qui suit est une explication supplémentaire de la formule, y compris la compréhension, les questions et la discussion.
Comprendre la formule ABC
La formule abc est l'une des formules utilisées pour trouver les racines d'une équation quadratique. Voici une forme générale de cette formule.

Les lettres a, b et c de la formule abc sont appelées coefficients. Le coefficient de x2 au carré est a, le coefficient de x est b et c est le coefficient de constante, généralement appelé terme constant ou indépendant.
L'équation quadratique est essentiellement une équation mathématique qui forme la géométrie incurvée de la parabole dans le quadrant xy.
La valeur du coefficient dans la formule abc a plusieurs significations comme suit:
- a détermine la prabole concave / convexe formée par l'équation quadratique. Si la valeur de a> 0, la parabole s'ouvrira vers le haut. Cependant, si a <0, la parabole s'ouvrira vers le bas.
- b détermine la position x du sommet de la parabole, ou la symétrie miroir de la courbe. La position exacte de l'axe de symétrie est -b / 2a de l'équation quadratique.
- c détermine le point d'intersection de la fonction d'équation quadratique parabolique formée sur l'axe y ou lorsque la valeur x = 0.
Exemples de questions et discussion
Voici quelques exemples de problèmes d'équations quadratiques et leur discussion avec des solutions utilisant des formules d'équations quadratiques.
1. Résous les racines de l'équation quadratique x2 + 7x + 10 = 0 en utilisant la formule abc!
Répondre:
Lisez aussi: 7 fonctions des protéines pour le corps [Explication complète]notez que a = 1, b = 7 et c = 10
alors, les racines de l'équation sont:

Ainsi, le produit des racines de l'équation x2 + 7x + 10 = 0 est x = -2 ou x = -5
2. À l'aide de la formule abc, trouvez l'ensemble des solutions pour x2 + 2x = 0
Répondre:
étant donné que a = 1, b = 1, c = 0
alors les racines de l'équation sont les suivantes:

Ainsi, le produit des racines de l'équation x2 + 2x = 0 est x1 = 0 et x2 = -2, donc l'ensemble de solutions est HP = {-2,0}
3. Trouvez l'ensemble des racines x dans le problème x2 - 2x - 3 = 0 en utilisant la formule abc
Répondre:
étant donné que a = 1, b = 2, c = -3
alors les résultats des racines de l'équation sont les suivants:

Ainsi, avec x1 = -1 et x2 = -3, l'ensemble des solutions est HP = {-1,3}
4. Déterminez le résultat de l'équation quadratique x 2 + 12x + 32 = 0 en utilisant la formule abc !
Répondre:
notez que a = 1, b = 12 et c = 32
alors les racines de l'équation sont les suivantes:

Ainsi, les résultats des racines de l'équation quadratique sont -4 et -8
5. Trouvez l'ensemble à partir du problème suivant 3x2 - x - 2 = 0
Répondre:
notez que a = 3, b = -1, c = -2
alors les racines de l'équation sont les suivantes:

Ainsi, les racines de l'équation quadratique 3x2 - x - 2 = 0 sont x1 = 1 et x2 = -2 / 3, donc l'ensemble de solutions est HP = {1, -2 / 3}
6. Trouvez les racines de l'équation x 2 + 8x + 12 = 0 en utilisant la formule abc!
Répondre:
notez que a = 1, b = 8 et c = 12
alors les racines de l'équation quadratique sont les suivantes:

Ainsi, les racines de l'équation quadratique x2 + 8x + 12 = 0 sont x1 = -6 ou x2 = -2 de sorte que l'ensemble des solutions est HP = {-6, -2}
7. Résous les racines de l'équation x 2 - 6x - 7 = 0 avec la formule abc .
Répondre:
on sait que a = 1, b = - 6 et c = - 7
alors les racines de l'équation sont les suivantes:
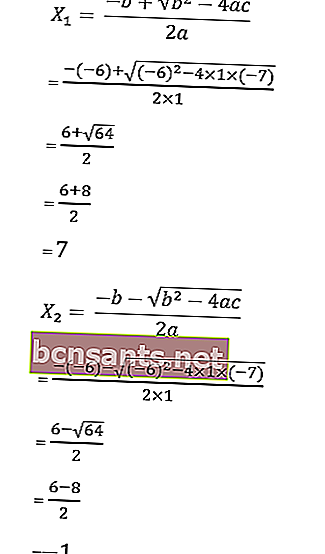
Donc, les racines sont x 1 = 1 ou x 2 = 5/2, donc l'ensemble des solutions est HP = {1, 5/2}.
Lisez aussi: Equations quadratiques (COMPLET): Définition, formules, exemples de problèmes8. Trouvez les racines de l'équation 2x 2 - 7x + 5 = 0 avec la formule abc
Répondre:
on sait a = 2, b = - 7 et c = 5
alors les racines de l'équation sont les suivantes:
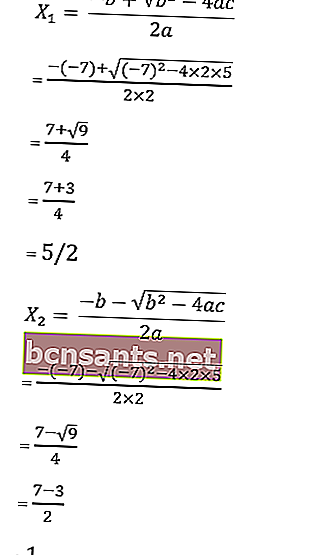
Les racines sont donc x1 = –4 ou x2 = 5/3 de sorte que l'ensemble des solutions est HP = {1, 5/3}.
9. Résolvez l'équation 3x 2 + 7x - 20 = 0 avec la formule abc.
Répondre:
sachant que a = 3, b = 7 et c = - 20
alors les racines de l'équation sont:
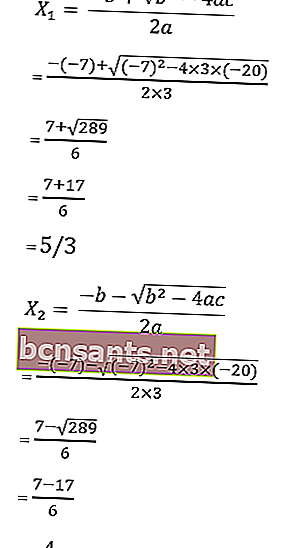
Donc les racines sont x1 = –4 ou x2 = 5/3, donc l'ensemble des solutions est HP = {-4, 5/3}.
10. Trouvez les racines de l'équation 2x 2 + 3x +5 = 0 avec la formule abc.
Répondre:
on sait que a = 2, b = 3 et c = 5
alors les racines de l'équation sont les suivantes:
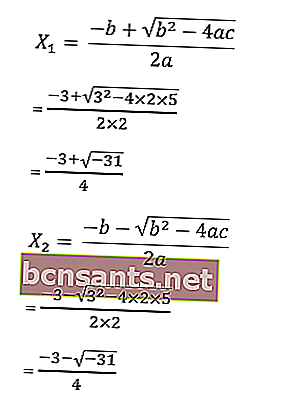
Le résultat de la racine de l'équation 2x2 + 3x +5 = 0 a le numéro de racine imaginaire √ - 31, donc l'équation n'a pas de solution. L'ensemble des solutions s'écrit l'ensemble vide HP = {∅}
Ceci est une explication de la définition de la formule abc avec des exemples de questions et leur discussion. Peut être utile!
